Problema11: Cartas de Control

Ej11. En una carta de control X, halla la probabilidad de que se presenten los siguientes sucesos:

a) Ocho puntos consecutivos de los cuales unos están a un lado u otros al otro lado de la línea central, pero todos fuera de los límites 1-sigma.

b) Quince puntos consecutivos entre los límites 1-sigma.


Realizamos una recopilación de datos ofrecidos por el enunciado del problema:

· Carta de control de medias X: X~N(μ, σ).

Pasamos a resolver los distintos apartados del problema propuesto.


Apartado a)

Calculamos la probabilidad de que un punto esté fuera de los límites 1-sigma, definimos el suceso:

A ≡ 'Un punto está fuera de los límites 1-sigma'.

Por lo tanto:

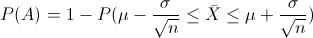
Al ser una carta de control de medias, sabemos que sigue una distribución Normal, por lo que tipifico:

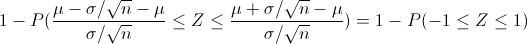
Por lo tanto:

P(A) = 1 - P(-1 < .Z < .1) = 1 - [(0.5+Φ(1)) - [1 - (0.5 + Φ(1))]] = 1 - 2·Φ(1)

Buscamos en la tabla de la Normal y obtenemos la probabilidad de que un punto esté fuera de los límites 1-sigma:

P(A) = 1 - 2·Φ(1) = 1 - 2·0.3413 = 0.3174

La probabilidad de que un punto esté fuera de los límites 1-σ es de 0.3174, pero el apartado nos pide la probabilidad de que ocho puntos consecutivos estén fuera de dichos límites, por lo tanto: (0.3174)⁸ ≈ 0.000103.

Apartado b)

Calculamos la probabilidad de que un punto esté dentro de los límites 1-σ, definimos el suceso:

B ≡ 'Un punto está dentro de los límites 1-sigma'.

Por lo tanto:

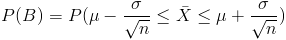
Al ser una carta de control de medias, sabemos que sigue una distribución Normal, por lo que tipifico:

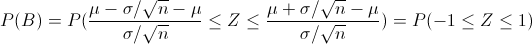
Por lo tanto:

P(B) = P(-1 < .Z < .1) = (0.5+Φ(1)) - [1 - (0.5 + Φ(1))] = 2·Φ(1)

Buscamos en la tabla de la Normal y obtenemos la probabilidad de que un punto esté dentro de los límites 1-sigma:

P(B) = 2·Φ(1) = 2·0.3413 = 0.6826

La probabilidad de que un punto esté dentro de los límites 1-σ es de 0.6826, pero el apartado nos pide la probabilidad de que quince puntos consecutivos estén dentro de dichos límites, por lo tanto: (0.6826)¹⁵ ≈ 0.003255.