Ej12. Un proceso industrial fabrica un sensor de velocidad para un controlador electrónico para frenos ABS. Las especificaciones de dicho sensor requieren que su impedancia sea de 30 kΩ ± 10 kΩ.
Para realizar el control estadístico de ese proceso se recogen muestras de 6 sensores cada media hora. Con los datos de un total de 30 muestras se obtiene la siguiente información: x = 30.11, R = 5.40.
Determinar:
a) Las características de control de la carta de medias X y de rangos R.
b) Calcular el cociente de capacidad del proceso e interprete su valor.
c) Si se produjese un cambio en la media de +3 kΩ, ¿Cuál es la probabilidad de detectar el cambio en la siguiente muestra?
Realizamos una recopilación de datos ofrecidos por el enunciado del problema:
· Límite superior de especificación: LSE = 30+10 = 40.
· Límite inferior de especificación: LIE = 30-10 = 20 .
· Límite central de la carta de medias X: LC = 30.11.
· Límite central de la carta de rangos R: LC = 5.40.
· Número de muestras: n = 6 cada media hora.
· Se desconoce μ y σ.
Pasamos a resolver los distintos apartados del problema propuesto.
Apartado a)
· Para la carta de control de medias X:
Nos piden obtener la carta de control de medias X, cuyos límites de control son:
·
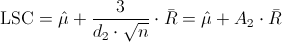
·
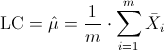
·
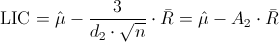
Donde A2 y d2, están tabulados para varios valores de n, en nuestro caso, n = 6, consultamos en la tabla:
· A2 = 0.483
· d2 = 2.534
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de medias X:
· LSC = μ + A2·R = 30.11 + 0.483·5.40 = 32.7182
· LC = μ = 30.11
· LIC = μ - A2·R = 30.11 - 0.483·5.40 = 27.5018
Como resumen, los límites de control para la carta X son:
· LSC = 32.7182
· LC = 30.11
· LIC = 27.5018
Los límites de control del proceso son:
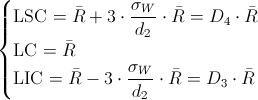
Donde D4 y D3, están tabulados para varios valores de n, en nuestro caso, n = 6, consultamos en la tabla:
· D4 = 2.004
· D3 = 0.00
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de rangos R:
· LSC = D4·R = 2.004·5.40 = 10.8216
· LC = R = 5.40
· LIC = D3·R = 0·5.40 = 0.00
Como resumen, los límites de control para la carta R son:
· LSC = 10.8216
· LC = 5.40
· LIC = 0
Apartado b)
El cociente de capacidad del está definido por la expresión:
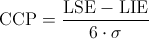
Donde σ vale:
Sigma: σ = R/d2 = 5.40/2.534 ≈ 2.131018
Por lo tanto, el coeficiente de capacidad del proceso vale:
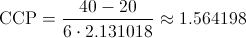
Al ser CCP > 1, existen pocas unidades defectuosas.
Apartado c)
En este apartado nos piden obtener la probabilidad de que un punto esté fuera de los límites 3-σ, definimos el suceso:
A ≡ 'Un punto está fuera de los límites de control 3-sigma'.
Donde la nueva media es:
· μ = 30.11+3 = 33.11.
Por lo tanto, la probabilidad que debemos hallar es:
Al ser una carta de control de medias, sabemos que sigue una distribución Normal, por lo que tipifico:
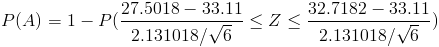
Aproximadamente es:
Por lo tanto:
Simplificamos:
Buscamos en la tabla de la Normal y obtenemos la probabilidad que nos piden en este apartado:
La probabilidad de que un punto esté fuera de los límites 3-σ es de 0.6736.





9 comentarios:
Hola, me gustaría saber de que tablas sacas A2, d2, D3 y D4 porfavor que necesito esas constantes
Buenas Jorge:
Las constantes que mencionas están tabuladas dependiendo del valor de n.
Dichas tablas son las que puedes descargar en cada capítulo del apartado Estadística, concretamente para las Cartas de Control, éste es el enlace:
http://unbarquero.blogspot.com/2009/05/cartas-de-control.html
Espero que te sea de utilidad.
Un saludo.
Buenas,
donde podria encontrar mas ejercicios de este tipo? me examino de estadistica en septiembre y me está ecostando mucho encontrar a alguien que pueda ayudarme con este tema ya que son ejercicios muy especificos (de un master) pero este es muy parecido a uno de los que caen en mis examenes. Gracias!!!
Buenas:
Generalmente en cualquier libro de estadística general podrás encontrar un tema dedicado al estudio de sucesos mediante cartas de control 3-sigma.
Aquí, en el blog, tenemos un tema dedicado que hasta ahora, contiene 20 problemas.
Un saludo.
Hola! no me habia dado cuenta! me vienen estupendamente. Mil gracias
Holaa! Solo queria preguntar, por que en este ejercicio cuando tipific usted, en el denominador de ambos parametros divide por (2,131018/raizde6) porque divide tambien entre raiz de 6, si la varianza es solo 2.131018?? Gracias!
Buenas:
Porque hay que tipificar los datos a la distribución Normal, y por definición, el estadístico es el siguiente:
· Z = [(X - μ)/(σ/√n]
Escrito de otra manera, quizás más reconocible y fácil de usar, es la siguiente:
· Z = [(X - μ)/σ]·√n
Ambas formas son idénticas.
Un saludo.
Gracias por su respuesta tan rapida, pero echando un ojo a mis apuntes y a los suyos (disponibles en esta pagina) no veo que aparezca en la formula de tipificar, del tema VARIABLES CONTINUAS, el parametro raiz de n. ¿Es por qué en este caso se trata de un estadistico y en el tema de variables continuas no? Gracias.
Buenas:
En el apartado de Variables Aleatorias Continuas, se tipifica mediante la distribución Normal estándar, pero en este caso, tenemos una muestra aleatoria de tamaño n, por lo que aplicamos la Teoría Central del Límite, que dice:
· Sea X1, X2, ..., Xn una muestra aleatoria de tamaño n de una distribución con media μ y varianza σ^2. Entonces, el límite de la distribución es:
· Z = [(X - μ)/σ]·√n
Este tipo de tipificación (la aproximación a la distribución Normal estándar), la podrás encontrar en el apartado: Estimación, Intervalos de Confianza y Pruebas de Hipótesis.
Un saludo.
Publicar un comentario