Ej13. Para controlar el proceso de fabricación de piezas metálicas se establece un control para la variable resistencia a la tensión mediante gráficos de control de medias y rangos. Se ha comprobado que la variable tiene una distribución normal.
Para diseñar los gráficos de control se han tomado 30 muestras de tamaño n = 6 con los siguientes resultados:
· Σxi = 6000.
· ΣRi = 150.
Determinar:
a) Las características de control de la carta de medias X y de rangos R.
b) Calcular el cociente de capacidad del proceso e interprete su valor.
c) Si se desajusta el proceso y fabrica con media igual a 199, ¿cuál es la probabilidad de detectar el cambio con el diagrama de la media en la muestra siguiente?. Obtenga el LDP.
Realizamos una recopilación de datos ofrecidos por el enunciado del problema:
· Límite central de la carta de medias X: LC = 6000/30 = 200.
· Límite central de la carta de rangos R: LC = 150/30 = 5.
· Número de muestras: n = 6.
· Se desconoce μ y σ.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
· Para la carta de control de medias X:
Nos piden obtener la carta de control de medias X, cuyos límites de control son:
·
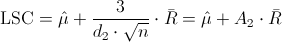
·
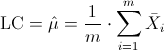
·
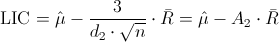
Donde A2 y d2, están tabulados para varios valores de n, en nuestro caso, n = 6, consultamos en la tabla:
· A2 = 0.483
· d2 = 2.534
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de medias X:
· LSC = μ + A2·R = 200 + 0.483·5 = 202.415
· LC = μ = 200
· LIC = μ - A2·R = 200 - 0.483·5 = 197.585
Como resumen, los límites de control para la carta X son:
· LSC = 202.415
· LC = 200
· LIC = 197.585
Los límites de control del proceso son:
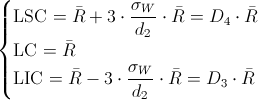
Donde D4 y D3, están tabulados para varios valores de n, en nuestro caso, n = 6, consultamos en la tabla:
· D4 = 2.004
· D3 = 0.00
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de rangos R:
· LSC = D4·R = 2.004·5 = 10.02
· LC = R = 5
· LIC = D3·R = 0·5 = 0.00
Como resumen, los límites de control para la carta R son:
· LSC = 10.02
· LC = 5
· LIC = 0
Apartado b)
Los límites de especificación son:
· Límite superior de especificación: LSE = 200+5 = 205.
· Límite inferior de especificación: LIE = 200-5 = 195 .
El cociente de capacidad del está definido por la expresión:
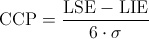
Donde σ vale:
Sigma: σ = R/d2 = 5/2.534 ≈ 1.973165
Por lo tanto, el coeficiente de capacidad del proceso vale:
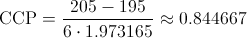
Al ser CCP < .1, existe un número grande de unidades que no cumple las especificaciones.
Apartado c)
En este apartado nos piden obtener la probabilidad de que un punto esté fuera de los límites 3-σ, definimos el suceso:
A ≡ 'Un punto está fuera de los límites de control 3-sigma'.
Donde la nueva media es:
· μ = 199.
Por lo tanto, la probabilidad que debemos hallar es:
Al ser una carta de control de medias, sabemos que sigue una distribución Normal, por lo que tipifico:
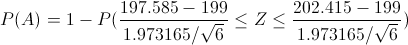
Aproximadamente es:
Por lo tanto:
Simplificamos:
Buscamos en la tabla de la Normal y obtenemos la probabilidad que nos piden en este apartado:
La probabilidad de detectar el cambio con el diagrama de la media en la muestra siguiente es de 0.0392.
Para obtener el parámetro LDP, empleamos su expresión matemática:
Por lo tanto, harán falta 25.510204 puntos en la gráfica para encontrar una anomalía.





2 comentarios:
Porqué a veces al tipificar la normal divides entre raiz del numero de muestras y por ejemplo en el ejercicio 19 no lo haces?
Gracias.
Un saludo.
Buenas:
Porque a diferencia del Problema 19, aquí estamos trabajando con parámetros normales, en el Problema 19, el parámetro es discreto y sigue una distribución Binomial, que al cumplirse las condiciones necesarias, podemos transformarlo a una distribución Normal.
Pero dicha transformación debe seguir ciertos patrones, el cual, se explica en el Capítulo: Variables Aleatorias Continuas y Distribuciones de Probabilidad.
Un saludo.
Publicar un comentario