Ej15. La característica de calidad de un determinado artículo tiene distribución normal. Se construye una carta X, tomando muestras de tamaño 4.
Las medias y los recorridos muestrales son los de la siguiente tabla:
| Muestra | X | R | Muestra | X | R | |
| 1 | 2.2 | 0.8 | 11 | 2.8 | 1.4 | |
| 2 | 2.0 | 1.8 | 12 | 1.9 | 1.6 | |
| 3 | 2.1 | 1.1 | 13 | 2.9 | 0.4 | |
| 4 | 2.2 | 1.1 | 14 | 2.4 | 1.1 | |
| 5 | 2.5 | 1.0 | 15 | 2.6 | 1.1 | |
| 6 | 2.9 | 0.6 | 16 | 2.1 | 2.0 | |
| 7 | 2.9 | 2.1 | 17 | 2.7 | 2.1 | |
| 8 | 2.6 | 1.6 | 18 | 2.5 | 1.1 | |
| 9 | 2.2 | 1.5 | 19 | 2.6 | 1.8 | |
| 10 | 2.8 | 1.1 | 20 | 2.4 | 1.6 |
Determinar:
a) Los límites de control 3-sigma, y úselos para estimar la media y la desviación típica de X.
b) Halle la LDP cuando la media aumenta hasta el valor 2.6.
Apartado a)
Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:
· Se desconoce μ y σ.
· Tamaño de la muestra: n = 4.
· Número de muestras: m = 20.
Nos piden obtener la carta de control de medias X, cuyos límites de control son:
·
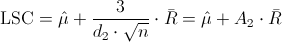
·
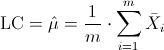
·
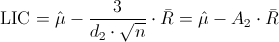
Donde A2 y d2, están tabulados para varios valores de n, en nuestro caso, n = 4, consultamos en la tabla:
· A2 = 0.729
· d2 = 2.059
Siendo:
·
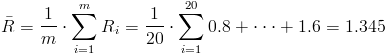
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de medias X, empezamos por la línea central:
·
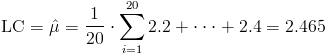
Y posteriormente, obtenemos los límites superior e inferior de control:
· LSC = μ + A2·R = 2.465 + 0.729·1.345 = 3.445505
· LIC = μ - A2·R = 2.465 - 0.729·1.345 = 1.484495
Como resumen, los límites de control para la carta X son:
· LSC = 3.445505
· LC = 2.465
· LIC = 1.484495
No nos piden que representemos la carta de control X, pero lo vamos hacer ya que en el proceso de diseño vamos a obtener el valor de la desviación típica.
Para representar la carta de control de medias, debemos obtener, previamente, los límites σ y 2·σ de las mismas para su posterior análisis mediante el método: Western Electric Handbook 1956.
Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.
En este caso, vamos a calcular el valor de σ para obtener los límites de control de advertencia.
- Para la carta X:
Sigma: σ = R/d2 = 1.345/2.059 ≈ 0.653230
Por lo tanto, los límites de advertencia de control 2σ son:
· X + 2·σ/√n = 2.465 + 2·0.653230/√4 = 3.11823
· X - 2·σ/√n = 2.465 - 2·0.653230/√4 = 1.81177
Para los límites de advertencia de control σ son:
· X + σ/√n = 2.465 + 0.653230/√4 = 2.791615
· X - σ/√n = 2.465 - 0.653230/√4 = 2.138385
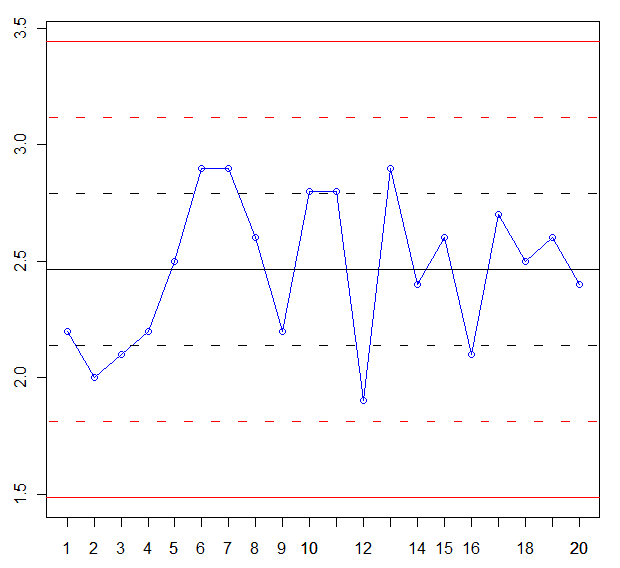
Y en este momento, estamos en disposición de realizar la gráfica de control X:
Pero el proceso está fuera de control ya que existen 4 de 5 puntos consecutivos que se encuentra a una distancia σ o más de la línea central. Los puntos son:
· 10: +σ
· 11: +σ
· 12: -σ
· 13: +σ
· 14: -LSC
Por lo tanto, el proceso X está fuera de control.
Apartado b)
En este apartado nos piden obtener el LDP del proceso donde la nueva media es:
· μ = 2.6.
Por lo tanto, la probabilidad que debemos hallar, para calcular posteriormente el LDP, es:
P(A) = P(LIC ≤ X ≤ LSC) = P(1.484495 ≤ X ≤ 3.445505)
Al ser una carta de control de medias, sabemos que sigue una distribución Normal, por lo que tipifico:
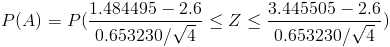
Aproximadamente es:
P(A) ≈ P(-3.42 ≤ Z ≤ 2.59)
Por lo tanto:
P(A) = P(-3.42 ≤ Z ≤ 2.59) = (0.5+Φ(2.59)) - [1 - (0.5+Φ(3.42))]
Simplificamos:
P(A) = Φ(2.59) + Φ(3.42)
Buscamos en la tabla de la Normal y obtenemos la probabilidad deseada:
P(A) = Φ(2.59) + Φ(3.42) = 0.4952 + 0.4997 = 0.9949
Para obtener el parámetro LDP, empleamos su expresión matemática:
LDP = 1/(1-P(A)) = 1/(1-0.9949) ≈ 196.078431.
Por lo tanto, harán falta 196.078431 puntos en la gráfica para encontrar una anomalía.





6 comentarios:
Hola! Una pregunta. La LDP es mayor en cartas con limite 2 sigma o en cartas con limite 3 sigma? O es igual en ambos casos? Gracias
Me refiero a si una con respecto a otra: aumenta, disminuye...
Buenas A. Bella:
El LDP nos dice cuantos puntos debemos contar para encontrar una anomalía en la gráfica.
Por lo tanto, no es un parámetro que, así a bote pronto, esté asociado directamente con la anchura de los límites de control, está asociado a la probabilidad de encontrar un punto fuera de dichos limites.
Por otro lado, el límite 2-sigma es un límite de advertencia mientras que el límite 3-sigma es un límite donde si un punto queda fuera de él, el proceso está fuera de control. Es por ello que el proceso de obtener el parámetro LDP se aplique al límite 3-sigma.
Un saludo.
¿Por que no interpola los resultados de la tipificacion? Ya que no salen unos numeros exactos como: 2,34 o 1,75 por ejemplo.
Muchas gracias.
Holaa muy buenas, ¿por qué no interpolas los valores obtenidos a tipificar? ya que los valores no son de la forma: 3.45 o 0.43 si no de mas decimales. Gracias y un saludo!
Buenas:
Es cierto que para ser más precisos, es necesario interpolar los datos.
En este caso, he optado por el redondeo que es también, una técnica válida. Y he optado por la aproximación para que la solución del ejercicio sea lo más clara posible.
Si interpolas, el resultado obtenido deberá ser muy parecido.
Un saludo.
Publicar un comentario