Problema20: Análisis de Regresión

Ej20. Los siguientes datos son observaciones sobre los caballos de vapor de un motor a 1800 rpm en función de la viscosidad del aceite:

HP	Viscosidad		HP	Viscosidad
16.3	43		19.0	57
16.4	44		18.1	59
16.8	45		18.8	61
17.0	47		18.2	62
16.9	48		19.2	63
17.5	49		18.5	66
16.7	50		20.2	67
18.1	54		21.2	67
18.6	55		19.7	68
17.7	56		22.2	70

Determinar:

a) Calcula las estimaciones de los coeficientes de regresión.

b) Halle el intervalo de confianza del 99% para la media de los caballos de vapor cuando la viscosidad es de 60.

c) Prueba la hipótesis de que la pendiente sea nula. ¿Es significativa la regresión?.


Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.

· n = 20

·

·

·

·

·

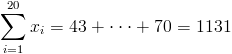
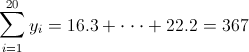
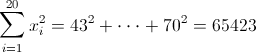
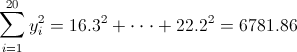
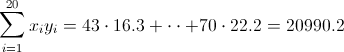
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Para calcular la pendiente, la expresión matemática es:

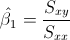
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·

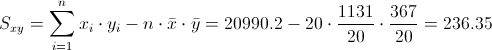
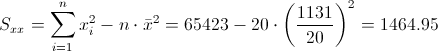
Por lo tanto, la pendiente es:

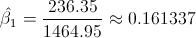
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:

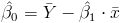
Sustituimos valores:

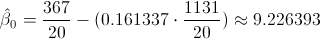
Por lo tanto, la ecuación de regresión ajustada es:

y(x) = 9.226393 + 0.161337·x

Siendo:

· y ≡ HP.
· x ≡ Viscosidad.

Apartado b)

En este apartado nos piden obtener un intervalo para la respuesta media, cuya expresión matemática es:

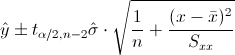
Al 99%, obtenemos α:

100(1 - α) = 99

Despejamos el parámetro que nos interesa: α = 0.01, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.01/2, 20 -2} = t_{0.005, 18} = 2.878

Debemos obtener el valor del estimador de la desviación estándar:

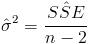
Siendo:

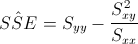
Debemos obtener Syy:

·

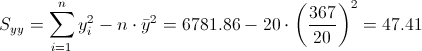
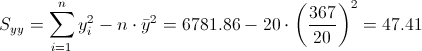
Ya tenemos todos los datos necesarios para estimar la varianza:

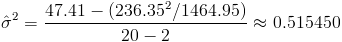
El único dato que nos falta por obtener es el valor del parámetro Y cuando x vale 60, para ello, usamos la recta ajustada calculada en el Apartado a):

· Y(60) = 9.226393 + 0.161337·60 = 18.906613.

Sustituimos valores en la expresión del interválo de confianza para la respuesta media

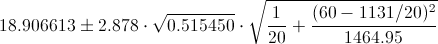
Por lo tanto, el intervalo de predicción al 99% es,aproximadamente:

[18.408457, 19.404769]

Apartado c)

Para estudiar si la regresión es significativa, la pendiente debe ser distinta de cero. Calcularemos tanto la región crítica como el p-valor, para contrastar los resultados.

La prueba de hipótesis es:

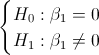
El estadístico es:

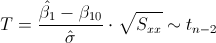
Disponemos de todos los datos necesarios, calculado en los apartados anteriores, para obtener el valor del estadístico:

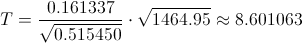
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

|T| > t_{α/2, n -2}

Al 99%, obtenemos α:

100(1 - α) = 99

Despejamos el parámetro que nos interesa: α = 0.01, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.01/2, 20 -2} = t_{0.005, 18} = 2.878

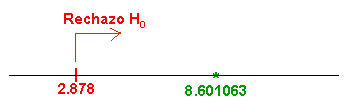
Comprobamos el valor del estadístico con la región crítica:

Se cumple la condición de la región crítica, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, la pendiente no vale cero, por lo tanto, existen evidencias significativas de que hay regresión lineal.

Ahora, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(T > |t|) = 2 · P(T > 8.601063)

Si buscamos, con 18 grados de libertad, en las tablas t-Student, no encontramos un valor exacto ni superior, sólo un nivel inferior, que corresponde al área de cola: 0.0005.

Por lo tanto, el área de cola será menor que 0.0005, el p-valor corresponderá:

p-valor < . 0.0010

Al ser el nivel de significación del problema, α = 0.01, mayor que el p-valor, rechazamos la hipótesis nula.

Rechazar la hipótesis nula quiere decir que se acepta la hipótesis alternativa, en otras palabras, la pendiente es distinta de cero por lo que existe evidencia significativa de que hay regresión lineal.

Como se puede observar, ambos métodos, la región crítica como el p-valor, satisfacen la hipótesis alternativa, es decir, que existe evidencias significativas que hay regresión lineal en el modelo obtenido.