Problema19: Cartas de Control

Ej19. Usando muestras de tamaño 400, se ha construido una carta de control de fracción de artículos defectuosos, para la cual se han tomado 30 muestras que han proporcionado un total de ΣD = 1200 artículos defectuosos.

a) Calcula los límites de control y la línea central de esta carta.

b) Halla el LDP estando el proceso bajo control.

c) Halla el LDP que permita detectar una desviación hasta un valor de 0.15 de la fracción media de artículos defectuosos.


Realizamos una pequeña recopilación de datos que nos ofrece el enunciado del problema:

· Sumatorio del número de artículos defectuosos: ΣD = 1200.
· Carta de fracción de artículos defectuosos, estamos hablando de una carta p.
· Tamaño de la muestra: n = 400.
· Número de muestras tomadas: m = 30.

Pasamos a resolver los distintos apartados del problema.


Apartado a)

Nos piden obtener la carta de control de fracción de defectos p, cuyos límites de control son:

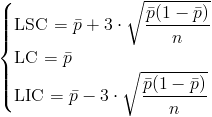
Siendo:

·

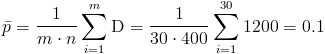
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de fracción defectuosos, p:

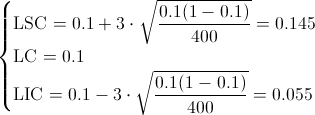
Apartado b)

En este apartado debemos obtener el LDP del proceso, definimos el evento:

· A ≡ Punto de la carta de control que queda fuera de los límites de control 3σ.

La expresión del parámetro LDP es:

LDP = 1/P(A)

Debemos obtener la probabilidad de que un punto quede fuera de los límites de control 3σ:

Teniendo en cuenta que:

·

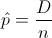
Siendo D, el número de unidades defectuosas en una muestra aleatoria de tamaño n. El evento D, sigue una distribución binomial: D ~ B(n, p).

Sustituimos:

P(A) = 1 - P(n·LIC ≤.D ≤.n·LSC)

Sustituimos valores:

P(A) = 1 - P(400·0.055 ≤.D ≤.400·0.145) = 1 - P(22 ≤.D ≤.58)

Recordemos que el evento D sigue una distribución binomial: D ~ B(400, 0.1), comprobamos si se puede aproximar a la Normal:

· μ = n·p = 400·0.1 = 40 ≥ 5
· n·p·q = 400·0.1(1-0.1) = 360 ≥ 5
· n = 400 > 25

Cumple con las condiciones necesarias para poder aproximar la binomial a la Normal, aplicamos el corrector por continuidad:

·

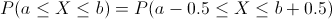
Por lo tanto, obtenemos:

· μ = n·p = 400·0.1 = 40
· σ = √(n·p·q) = √(400·0.1·(1-0.1) = 6

Tipificamos a la Normal teniendo en cuenta el corrector por continuidad:

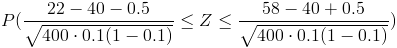
Aproximadamente es:

P(A) ≈ 1 - P(-3.08 ≤ Z ≤ 3.08)

Simplificamos:

P(A) = 1 - [(0.5 + Φ(3.08)) - [1 - (0.5 + Φ(3.08))]] = 1 - 2·Φ(3.08)

Busco en la tabla de la Normal y obtengo la probabilidad de que un punto quede fuera de los límites de control 3σ:

P(A) = 1 - 2Φ(3.08) = 1 - 0.4990 - 0.4994 = 0.002

En estos momentos, disponemos de todos los datos necesarios para obtener el LDP:

LDP = 1/P(A) = 1/0.002 = 500

Se necesitan 500 puntos para observar uno, fuera de los límites de control 3σ.


Apartado c)

En este apartado debemos obtener, nuevamente el LDP del proceso, pero teniendo en cuenta que la media se ha incrementado hasta el valor:

· ṗ = 0.15

Procedemos igual que en el apartado anterior pero esta vez, con la nueva media, definimos el evento:

· A ≡ Punto de la carta de control que queda fuera de los límites de control 3σ.

La expresión del parámetro LDP es:

LDP = 1/P(A)

Debemos obtener la probabilidad de que un punto quede fuera de los límites de control 3σ:

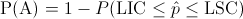
Teniendo en cuenta que:

·

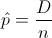
Siendo D, el número de unidades defectuosas en una muestra aleatoria de tamaño n. El evento D, sigue una distribución binomial: D ~ B(n, p).

Sustituimos:

P(A) = 1 - P(n·LIC ≤.D ≤.n·LSC)

Sustituimos valores:

P(A) = 1 - P(400·0.055 ≤.D ≤.400·0.145) = 1 - P(22 ≤.D ≤.58)

Recordemos que el evento D sigue una distribución binomial: D ~ B(400, 0.15), comprobamos si se puede aproximar a la Normal:

· μ = n·p = 400·0.15 = 60 ≥ 5
· n·p·q = 400·0.15(1-0.15) = 340 ≥ 5
· n = 400 > 25

Cumple con las condiciones necesarias para poder aproximar la binomial a la Normal, aplicamos el corrector por continuidad:

·

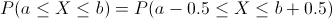
Por lo tanto, obtenemos:

· μ = n·p = 400·0.15 = 60
· σ = √(n·p·q) = √(400·0.15·(1-0.15) ≈ 7.141428

Tipificamos a la Normal teniendo en cuenta el corrector por continuidad:

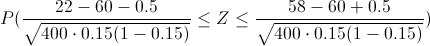
Aproximadamente obtenemos:

P(A) ≈ 1 - P(-5.39 ≤ Z ≤ -0.21)

Simplificamos:

P(A) = 1 - [[1 - (0.5 + Φ(3.08))] - [1 - (0.5 + Φ(3.08))]] = 1 - [Φ(5.39) - Φ(0.21)]

Busco en la tabla de la Normal y obtengo la probabilidad de que un punto quede fuera de los límites de control 3σ:

P(A) = 1 - [Φ(5.39) - Φ(0.21)] ≈ 1 - [0.5 - 0.0832] = 1 - 0.4168 = 0.5832

Hay que tener en cuenta que en las tablas que dispone Aqueronte no está el valor para 5.39, pero se ve, claramente que, aproximadamente es 0.5.

En estos momentos, disponemos de todos los datos necesarios para obtener el LDP:

LDP = 1/P(A) = 1/0.5832 ≈ 1.714678

Se necesitan, aproximadamente, 2 puntos para observar uno, fuera de los límites de control 3σ.

Para concluir el estudio vamos a obtener el porcentaje de aumento de la media de fracción de artículos defectuosos, en valor absoluto:

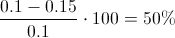
Al aumentarse la media de fracción de artículos defectuosos en un 50%, comprobaremos la reducción del LDP:

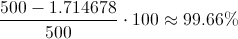
Se ha reducido el LDP en caso un 99.66%, una reducción bastante significativa.

Esto nos indica que al aumentarse a la mitad la media de fracción de artículos defectuosos, la probabilidad de encontrarse un punto fuera de los límites de control aumenta de manera significativa.