Ej38. La probabilidad de obtener dos bolas negras consecutivas elegida, previamente, una urna al azar entre dos posibles es de 19/90.
Determinar:
a) Si este experimento se repite 250 veces. ¿Cuál es la probabilidad de que el número de veces que sacamos dos bolas negras sea mayor que 60?
b) Cuántas veces debe repetirse el experimento para que, al menos en el 80% de los casos, el número de veces que se obtengan dos bolas negras sea superior a 50.
Apartado a)
Sea la variable aleatoria discreta X, número de veces que sacamos dos bolas negras. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:
La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(250, 19/90).
Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5 → 250·10/90 = 475/9 ≥ 5 OK.
2. n·q ≥ 5 → 250·(1-19/90) = 1775/9 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
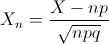
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(475/9, 6.452581).
En este apartado debemos obtener la siguiente probabilidad:
Aplicamos el factor de corrección:
Y en estos momentos estamos en condiciones de tipificar por la Normal:
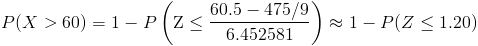
Obtenemos:
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
Por lo tanto, si repetimos este experimento 250 veces, la probabilidad de obtener dos bolas negras, sea más de 60 veces, es de 0.1151, una probabilidad baja.
Apartado b)
El enunciado nos ofrece la siguiente probabilidad: P(X > 50) ≥ 0.8, y debemos obtener el número de veces que se debe repetir el experimento para tal propósito, es decir, el parámetro n.
Despejamos:
Aplicamos el factor de corrección por tratarse de una variable discreta aproximada a la Normal:
Tipificamos:
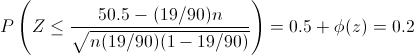
Despejamos Φ(z):
En las tablas que dispone este blog, Aqueronte, no se encuentran valores negativos, pero ésto no nos supone ningún inconveniente, ya que la curva de la Normal es simétrica, por lo que buscamos el valor 0.3 sabiendo que su resultado debe ser negativo.
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.3, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:
..0.84...........Z..... ..0.85
0.2995.....0.3.... .0.3023
De donde:
0.84 - 0.85.-> 0.2995 - 0.3023
0.84 - Z.-> 0.2995 - 0.3
Calculamos:
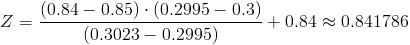
Teniendo en cuenta que estamos en la parte negativa de la curva, z = -0.841786.
Por lo tanto, tenemos:
Obtenemos una ecuación de segundo orden:
La resolvemos y obtenemos dos soluciones:
· n1 ≈ 265.728151.
· n2 ≈ 215.337052.
¿Cuál de las dos soluciones es válida? En nuestro caso será n1 (~265.728151), ya que es la solución que cumple con todos los pasos que hemos realizado anteriormente en este apartado hasta llegar a la solución.
¿Y por qué tenemos dos soluciones? Pues ya se ha comentado anteriormente algo, es simplemente porque la curva de la Normal es simétrica, esto hace que tengamos dos soluciones: una en su parte derecha y otra en su parte izquierda.
Por lo tanto, n debe ser un valor entero positivo, n > 265.

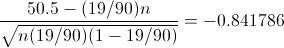




2 comentarios:
Hola, buenas tardes. En primer lugar felicitarle por el blog.
Me a surgido una duda, en este ejercicio. En la resolución, se aplica corrección; mientras que en el ejercicio 37, encontrándonos en el mismo caso (variable aleatoria discreta, en la cual se cumplen las restricciones necesarias), no se hace.
¿A qué es debido?. Gracias.
Buenas:
El problema no es el mismo, mientras que en el Problema38, debemos obtener el número de veces que debe repetir el experimento para tal propósito, en el Problema37, debemos obtener el valor del número de garajes necesarios para que se cumpla dicha probabilidad.
Es decir, en el Problema38 obtenemos el número de repeticiones pero ya teniendo el valor de n, mientras que en el Problema37, obtenemos el valor de n, los elementos necesarios para que se cumpla la probabilidad dada.
Un saludo.
Publicar un comentario