Ej1. Obtenga la transformada de Laplace de la siguiente función.
f(t) = 11 + 5·e4t - 6·sin(2t)
Lo primero que haremos es aplicar la ley de linealidad:
L{11 + 5·e4t - 6·sin(2t)} = 11·L{1} + 5·L{e4t} - 6·L{sin(2t)}
La Transformada de Laplace que debemos resolver, teniendo en cuenta la Tabla que dispone Aqueronte, son:
· Transformada de Laplace de una constante: f(t) = 1
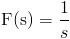
· Transformada de Laplace de la función del número e: f(t) = e4t
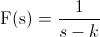
Siendo k = 4.
· Transformada de Laplace de la función seno: f(t) = sin(2t)
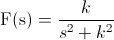
Siendo k = 2.
Sustituimos valores para resolver este problema:
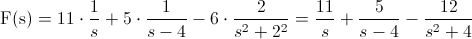





0 comentarios:
Publicar un comentario