Problema5: Laplace

Ej5. Obtenga la transformada de Laplace de la siguiente función.

f(t) = cos(k·t)

Siendo k una constante distinta de cero.

Nos piden obtener la transformada de la función coseno, pero vamos a calcular de un tirón, la transformada de las funciones coseno y seno. Ésto lo conseguiremos empleando la relación de Euler:

e^ikt = cos(k·t) + i·sin(k·t)

Por lo tanto, nuestra nueva función a obtener la transformada, es: f(t) = e^ikt

Utilizamos la propia definición de Transformada de Laplace:

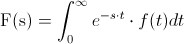
Y simplemente, debemos resolver dicha integral:

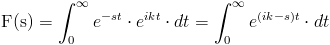
Realizamos el siguiente cambio de variable:

· x = (i·k-s)·t
· dx = (i·k-s)·dt

Para resolver de forma fácil la integral propuesta:

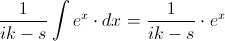
Deshacemos el cambio de variable:

· x = (i·k-s)·t

Para resolver el problema:

Se ha operado el siguiente término:

e^(ik-s)t = e^-(s-ik)t

Para ponerlo de una forma cómoda para resolver la integral, y ahora, multiplicamos por su conjugado para eliminar del denominador el operando imaginario:

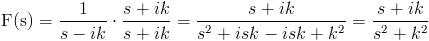
Llegados a este punto, se puede dar por resuelta la Transformada de Laplace de la fórmula o relación de Euler, y por consiguiente, se pueden extraer las transformadas de las funciones coseno y seno requeridas por este problema.

Para ello, igualamos las identidades, el coseno sería la parte real y el seno, la parte imaginaria.

· Transformada de Laplace de la función coseno: f(t) = cos(k·t)

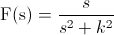
· Transformada de Laplace de la función seno: f(t) = sin(k·t)

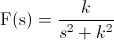
Existen otros métodos para llegar a la misma solución expuesta en este capítulo, pero a mi parecer, ésta es una de las más simples.