Ej4. Obtenga la transformada de Laplace de la siguiente función.
f(t) = t2
Para resolver este problema utilizamos la propia definición de Transformada de Laplace:
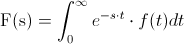
Y simplemente, debemos resolver dicha integral:
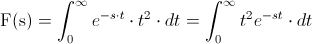
Resolvemos la integral por partes:
| · u = t2 | , | du = 2t |
| · dv= e-st | ,.. | v = -(1/s)e-st |
Resolvemos la integral:
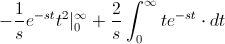
La integral que tenemos ahora, la volvemos a operarla por partes:
| · u = 2t | , | du = 2dt |
| · dv= e-st | ,.. | v = -(1/s)e-st |
Para resolver de forma fácil la integral propuesta:
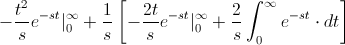
Ahora, podemos operar de forma fácil la integral:
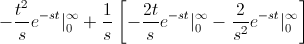
Tenemos dos problemas, con el primer y segundo término cuando t tiende a infinito:
· 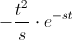
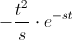
·
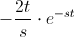
Ambas, son una indeterminación del tipo: ∞/∞. Para obtener su resultado, observaremos el valor en el límite, para ello, necesitaremos aplicar L'Hôpital:
· 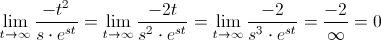
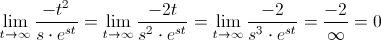
·
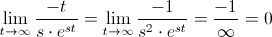
Pues ya disponemos de todos los datos necesarios para obtener la Transformada de Laplace de la función dada en este problema:
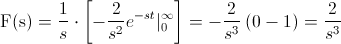
Para s > 0.





0 comentarios:
Publicar un comentario