Problema10: Laplace Tablas

Ej10. Obtenga la transformada de Laplace de la siguiente función.

f(t) = sin(2t)·sin(5t)

Para simplificar los cálculos, emplearemos relaciones trigonométricas para tal fin, concretamente: Producto Seno de Dos Ángulos Distintos.

· sin(α)·sin(β) = (1/2)·[cos(α-β)-cos(α+β)]

Siendo:

· α = 2t
· β = 5t

Ahora, la transformada que tenemos que obtener, después de emplear la relación trigonométrica, es la siguiente:

L{sin(2t)·sin(5t)} = (1/2)·L{cos(2t-5t) - cos(2t+5t)}

Aplicamos la propiedad de Linealidad:

L{sin(2t)·sin(5t)}=(1/2)·L(cos(2t-5t))-(1/2)·L(cos(2t+5t))= (1/2)·L(cos(-3t))-(1/2)·L(cos(7t))

Empleando las tablas que dispone Aqueronte, resolvemos la transformada de la función coseno.

· Transformada de Laplace de la función coseno: f(t) = cos(k·t)

L{cos(k·t)} = s/(s²+k²)

Siendo:

· Para el Primer miembro: k = -3.
· Para el Segundo miembro: k = 7.

En estos momentos, disponemos de todos los datos necesarios para obtener la solución a este problema, simplemente, sustituimos valores:

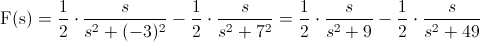
En este problema se demuestra que a veces es muy útil intentar manipular la función dada de tal forma que, se simplifique los cálculos posteriores para obtener su transformada.