Problema11: Laplace Tablas

Ej11. Obtenga la transformada de Laplace de la siguiente función.

f(t) = t⁴ - t² - t + sin(t·√2)

Lo primero que haremos es aplicar la propiedad de linealidad:

L{t⁴ - t² - t + sin(t·√2)} = L{t⁴} - L{t²} - L{t} + L{sin(t·√2)}

Para resolver la transformada, emplearemos tanto las tablas como las propiedades de esta herramienta.

· Transformada de Laplace de la función : f(t) = t⁴, lo que tenemos que hallar es:

L{t⁴)} = (n-1)!/sⁿ

Siendo n = 5.

· Transformada de Laplace de la función : f(t) = t², lo que tenemos que hallar es:

L{t²)} = (n-1)!/sⁿ

Siendo n = 3.

· Transformada de Laplace de la función : f(t) = t, lo que tenemos que hallar es:

L{t)} = (n-1)!/sⁿ

Siendo n = 2.

· Transformada de Laplace de la función : f(t) = sin(t·√2), lo que tenemos que hallar es:

L{sin(t·√2))} = k/(s²+k²)

Siendo k = √2.

En estos momentos, disponemos de todos los datos necesarios para obtener la Transformada de Laplace dada, simplemente, sustituimos valores:

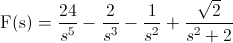
Este problema se ha resuelto empleando las tablas que este blog dispone.