Problema6: Laplace

Ej6. Obtenga la transformada de Laplace de la siguiente función.

f(t) = sinh(k·t)

Siendo k una constante distinta de cero.

Nos piden obtener la transformada de la función del seno hiperbólico, cuya definición viene dada por la siguiente expresión:

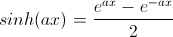
Utilizamos la propia definición de Transformada de Laplace:

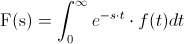
Y simplemente, debemos resolver dicha integral:

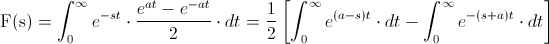
Realizamos los siguientes cambios de variables:

· x = (a-s)·t
· dx = (a-s)·dt

· y = -(s+a)·t
· dy = -(s+a)·dt

Para resolver de forma fácil la integral propuesta:

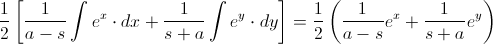
Deshacemos los cambios de variables:

· x = (a-s)·t
· y = -(s+a)·t

Para resolver el problema:

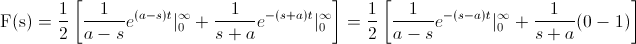
Seguimos operando:

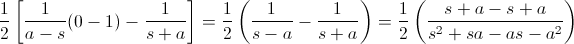
Simplificamos y obtenemos la solución a este problema:

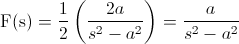
Este problema se puede resolver por tablas, pero la intención es mostrar cómo simplificar mediante las propiedades de la transformada, para resolverla de forma fácil.