Problema51: Probabilidad

Ej51. Una fábrica recibe pistones producidos por tres proveedores, A, B y C, los cuales producen el 40%, 35% y 25% de los mismos, respectivamente.

Se sabe que la producción del proveedor A tiene un 3% de defectuosos, la de la fábrica B un 2% de defectuosos y que en el conjunto de todos los pistones recibidos (provenientes de los tres proveedores) la proporción de defectuosos alcanza el 2.5%.

Hallar la probabilidad de que una pieza provenga del proveedor C, si se sabe que es defectuosa.


Realizamos una recopilación de datos dados por el enunciado del problema:

· A ≡ 'Proveedor A'.
· B ≡ 'Proveedor B'.
· C ≡ 'Proveedor C'.

· P(A) = 0.4.
· P(B) = 0.35.
· P(C) = 0.25.

· D ≡ 'Piezas defectuosas'.

· P(D|A) = 0.03.
· P(D|B) = 0.02.
· P(D) = 0.025.

Nos piden obtener la probabilidad de que una pieza provenga del proveedor C si se sabe que ésta, es defectuosa. Para tal fin, emplearemos la expresión de la probabilidad total, ya que nos dan su valor, para despejar el parámetro que nos requieren.

La probabilidad de piezas defectuosas es:

P(D) = P(D|A)·P(A) + P(D|B)·P(B) + P(D|C)·P(C)

Despejamos:

P(D|C)·P(C) = P(D) - P(D|A)·P(A) - P(D|B)·P(B) = 0.025 - 0.03·0.4 - 0.02·0.35 = 0.006

Una vez obtenido dicho parámetro, pasamos a resolver el problema mediante la Ley de Bayes:

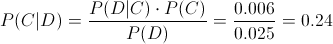
Por lo tanto, la probabilidad de que una pieza provenga del proveedor C dada que ésta, es defectuosa, es de 0.24.