Ej10. Obtenga la transformada inversa de Laplace de la siguiente función.
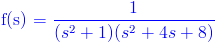
Descomponemos el denominador en fracciones:

Operamos:
1 =(As+B)(s2+4s+8)+(Cs+D)(s2+1)= As3 + 4As2 + 8As + Bs2 + 4Bs + 8B + Cs3 + Cs + Ds2 + D
Agrupamos por términos:
· s3: A+C = 0
· s2: 4A+B+D = 0
· s1: 8A+4B+C = 0
· s0: 8B+D = 1
Resolvemos el sistema formado por cuatro ecuaciones con cuatro incógnitas, dando como resultado:
· A = -4/65
· B= 7/65
· C = 4/65
· D = 9/65
Por lo tanto, la ecuación nos queda de la siguiente manera:
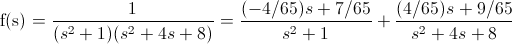
Simplificamos:

Expandimos la función de tal manera que sea medianamente reconocible a las funciones dadas en las tablas:
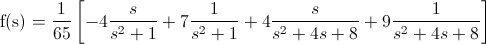
Para el tercer y cuarto miembro, el denominador presenta la siguiente estructura:
a·s2 + b·s + c
Identificamos los elementos:
· a = 1
· b = 4
· c = 8
Podemos completar cuadrados si la agrupamos de la siguiente forma:
a·(s+k)2 + h2
Siendo:
·
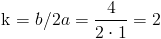
·
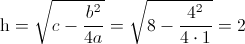
Por lo tanto, tenemos:
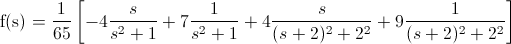
En estos momentos, estamos en disposición de identificar cada miembro de la función acorde a las dadas en las tablas.
• Primer Miembro: Transformada de Laplace de la función: f(t) = cos(k·x)
L{cos(k·x)} = s/(s2+k2)
Siendo:
· k = 1.
• Segundo Miembro: Transformada de Laplace de la función: f(t) = sin(k·x)
L{sin(k·x)} = k/(s2+k2)
Siendo:
· k = 1.
• Tercer Miembro: Transformada de Laplace de la función: f(t) = eb·x·cos(k·x)
L{eb·x·cos(k·x)} = (s-b)/[(s-b)2+k2]
Siendo:
· b = -2.
· k = 2.
• Cuarto Miembro: Transformada de Laplace de la función: f(t) = eb·x·sin(k·x)
L{eb·x·sin(k·x)} = k/[(s-b)2+k2]
Siendo:
· b = -2.
· k = 2.
La antitransformada del primer y segundo miembro son inmediatas mientras que, la del tercer y cuarto miembro deben ser adaptadas para obtener la función que deseamos:

Expandimos el tercer miembro:

En estos momentos, la antitransformada de los miembros, son inmediatas:

Simplificamos para obtener la solución a este problema:

Normalmente, como se suele observar en este problema, para obtener la transformada inversa deberemos manipular la expresión para llegar a una solución adecuada.





0 comentarios:
Publicar un comentario