Problema9: Inversa de Laplace

Ej9. Obtenga la transformada inversa de Laplace de la siguiente función.

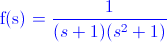
El denominador presenta la siguiente estructura:

(s² + b·s + c)^p

Debemos expresar la función de la siguiente forma:

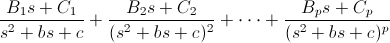
Descomponemos el denominador en fracciones:

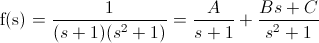
Operamos:

1 = A(s²+1) + (Bs+C)(s+1) = As² + A + Bs² + Bs + Cs + C

Agrupamos por términos:

· s²: A+B = 0
· s¹: B+C = 0
· s⁰: A+C = 1

Resolvemos el sistema formado por tres ecuaciones, dando como resultado:

· A = 1/2
· B= -1/2
· C = 1/2

Por lo tanto, la ecuación nos queda de la siguiente manera:

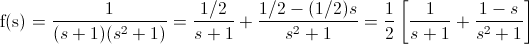
Operamos para poner el segundo miembro de una manera fácil de reconocer en las tablas:

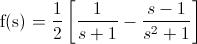
Expando la función:

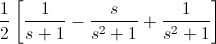
Para el primer miembro, lo podemos adaptar para la función exponencial, pero en esta ocasión, vamos a dar cierto rodeo, vamos a multiplicarlo por su conjugado:

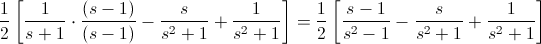
Expandimos el primer miembro:

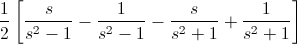
En estos momentos, estamos en disposición de identificar cada miembro de la función acorde a las dadas en las tablas.

• Primer Miembro: Transformada de Laplace de la función: f(t) = cosh(k·x)

L{cosh(k·x)} = s/(s²-k²)

Siendo:

· k = 1.

• Segundo Miembro: Transformada de Laplace de la función: f(t) = sinh(k·x)

L{sinh(k·x)} = k/(s²-k²)

Siendo:

· k = 1.

• Tercer Miembro: Transformada de Laplace de la función: f(t) = cos(k·x)

L{cos(k·x)} = s/(s²+k²)

Siendo:

· k = 1.

• Cuarto Miembro: Transformada de Laplace de la función: f(t) = sin(k·x)

L{sin(k·x)} = k/(s²+k²)

Siendo:

· k = 1.

Por lo tanto, la antitransformada que debemos obtener es la siguiente:

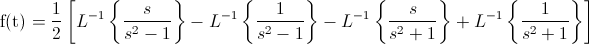
La antitransformada de los miembros, son inmediatas:

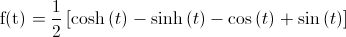
Normalmente, como se suele observar en este problema, para obtener la transformada inversa deberemos manipular la expresión para llegar a una solución adecuada.