Ej43. En un quiosco de periódicos se supone que el número de ventas diarias se distribuye normalmente con media 30 y varianza 2.
Determinar:
a) Probabilidad de que en un día se vendan entre 13 y 31 periódicos.
b) Determinar el máximo número de periódicos que se venden en el 90% de las ocasiones.
Sea la variable aleatoria X, número de ventas diarias de periódicos en cierto quiosco. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 30 y la desviación estándar: √2.
Pasamos a resolver los distintos apartados ofrecidos.
Apartado a)
Debemos obtener la siguiente probabilidad:
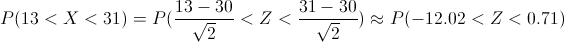
Operamos:
P(13 < .X < .31) ≈ P(-12.02 < .Z < .0.71) = (0.5+Φ(0.71))-[1-(0.5+Φ(12.02))] = Φ(0.71)+Φ(12.02)
Buscamos en las tablas de la Normal expuestas en este blog, para dar cómo resultado final:
P(13 < .X < .31) = Φ(0.71) + Φ(12.02) = 0.2580 + 0.5 = 0.7580
Por lo tanto, la probabilidad de que la venta de periódicos esté comprendida entre 13 y 31 ejemplares diarios es de 0.7580.
Apartado b)
En este apartado, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria X que lo satisfaga.
Tenemos: P(X ≤ x) = 0.9
Operamos:
P(X ≤ x) = 0.5 + Φ(z) = 0.9
Despejamos:
Φ(z) = 0.9 - 0.5 = 0.4
Buscamos en las tablas de la Normal el valor 0.4, pero en este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.28.............Z..........1.29
0.3997........0.4.....0.4015
De donde:
0.3997 - 0.4015.-> 1.28 - 1.29
0.3997 - 0.4..-> 1.28 - Z
Calculamos:
Por lo tanto, la venta de periódicos diarias para el quiosco en cuestión será de:
1.281667 = (x - 30)/√2
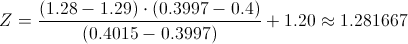
Despejamos x:
x ≈ 31.812551
Como no se puede vender medio periódico, la solución a este apartado es: x ≥ 32 periódicos diarios.
3 comentarios:
Tengo una duda respecto a la desigualdad que tu colocas 1.281667<(x-30)/2^(1/2), creo que hay un error porque al momento de estandarizar z=(x-u)/...
en vez de colocar la desigualdad creo que deberia ir una igualdad.
Buenas:
Tienes razón, es una igualdad.
Aunque en algunos libros lo encontrarás como una desigualdad y no está del todo mal, si tenemos en cuenta que estamos trabajando con variables continuas y por ende, lo que queremos obtener es el valor a partir del cual se cumplen dichas condiciones.
Un saludo.
Hola.
Es una tontería, pero en el apartado a) Φ(0.71) = 0.2611.
Un saludo y gracias por su blog.
Publicar un comentario