Ej42. La duración de un láser semiconductor a potencia constante tiene una distribución normal con media 7.000 horas y desviación típica de 600 horas.
Determinar:
a) ¿Cuál es la probabilidad de que el láser falle antes de 5.000 horas?.
b) ¿Cuál es la duración en horas excedida por el 95 % de los láseres?.
Sea la variable aleatoria X, duración de un láser semiconductor a potencia constante. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 7000 y la desviación estándar: 600.
Pasamos a resolver los distintos apartados ofrecidos.
Apartado a)
Debemos obtener la siguiente probabilidad:
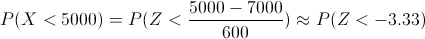
Operamos:
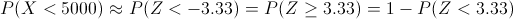
Despejamos:
P(Z < .3.33) = 1 - [0.5 + Φ(3.33)] = 0.5 - Φ(3.33)
Buscamos en las tablas de la Normal expuestas en este blog, para dar cómo resultado final:
P(Z < .3.33) = 0.5 - Φ(3.33) = 0.5 - 0.4996 = 0.0004
Por lo tanto, la probabilidad de que la duración del láser sea menos de 5000 horas es de 0.0004, es decir, una probabilidad baja, en conclusión, es más que probable que duré más de 5000 horas.
Apartado b)
En este apartado, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria X que lo satisfaga.
Tenemos: P(X >. x) = 0.95
Operamos:
1 - P(X ≤ x) = 0.95
Despejamos:
P(X ≤ x) = 1 - 0.95 = 0.05 = 0.5 + Φ(z)
Volvemos a despejar:
Φ(z) = 0.05 - 0.5 = -0.45
Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay problema ya que son simétricos, por lo que buscamos en la tabla el valor 0.45 que de un z válido.
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
0.4495 - 0.4505.-> 1.64 - 1.65
0.4495 - 0.45..-> 1.64 - Z
Calculamos:
Teniendo en cuenta que z se encuentra en la parte izquierda de la campana de Gauss, entonces: z = -1.645.
Por lo tanto, la duración del láser semiconductor de potencia constante será de:
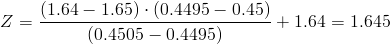
Por lo tanto, la duración del láser semiconductor de potencia constante será de:
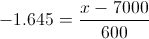
Despejamos x y obtenemos la solución a este problema: x = 6013 horas.
2 comentarios:
se te agradece brother gracias
ayuda con este ejercicio:
una maquina de refrescos se puede ajustar de manera que llene los vasos con μ cl. si la cantidad de liquido por vaso sigue una distribución normal, encontrar el parámetro de ajuste μ de manera que los vasos con capacidad máxima 30cl. se derramen con probabilidad 0,01 y que la cantidad de refresco que eche la maquina sea mayo que 22cl. con probabilidad 0,8
Publicar un comentario