Problema46: VAC

Ej46. Un banco recibe en promedio 6 cheques falsos al día, suponiendo que el número de cheques falsos sigue una distribución de Poisson, hallar:

a) Probabilidad de que se reciban cuatro cheques falsos en un día.

b) Probabilidad de que se reciban más de 30 cheques falsos en una semana.


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de cheques falsos que recibe un banco al día.
· La variable aleatoria discreta X sigue una distribución Poisson: X ~ P(6)

Resolvemos los apartados ofrecidos por este problema.


Apartado a)

Debemos obtener la siguiente probabilidad:

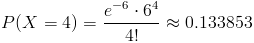
Por lo tanto, la probabilidad de que lleguen cuatro cheques al día en dicho banco es de, aproximadamente, 0.133853.


Apartado b)

En este caso, debemos adaptar el parámetro promedio ya que el enunciado se nos ofrece como cheques/diarios, pero en este apartado debemos obtener la probabilidad a la semana.

Teniendo en cuenta que una semana consta de siete días:

6 --- 1
λ --- 7

Por lo tanto, el valor promedio de cheques/semana es de: λ = (7·6)/1 = 42.

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:

1. λ > 25 → 42 > 25 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

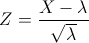
Por lo tanto: X ~ N(λ, √λ) = N(42, √42).

Debemos obtener la siguiente probabilidad:

P(X > 30) = 1 - P(X ≤ 30)

Aplicamos el factor de corrección:

P(X > 30) = 1 - P(X ≤ 30.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal: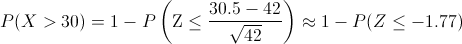

Obtenemos:

P(X > 30) = 1 - P(Z ≤ -1.77) = 1 - P(Z ≥ 1.77) = 1 - [1 - P(Z < .1.77)] = P(Z < .1.77)

Por lo tanto:

P(X > 30) = P(Z < .1.77) = 0.5 + Φ(1.77)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X > 30) = 0.5 + Φ(1.77) = 0.5 + 0.4616 = 0.9616

Por lo tanto, la probabilidad de que lleguen más de treinta cheques a la semana en dicho banco es de 0.9616, como podemos observar, una probabilidad alta.