Problema45: VAC

Ej45. La confianza de un fusible eléctrico corresponde a la probabilidad de que un fusible escogido al azar de una línea de producción, funcione adecuadamente bajo condiciones de diseño.

Calcule la probabilidad de obtener 27 ó mas fusibles defectuosos en una muestra de 1000 fusibles, sabiendo que la probabilidad de que un fusible elegido al azar no sea defectuoso es de 0.98.


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de fusibles defectuosos.
· Tamaño de la muestra: N = 1000 fusibles.
· Probabilidad de que un fusible sea defectuoso: p = 1-q = 1-0.98 = 0.02.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(1000, 0.02)

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 1000·0.2 = 20 ≥ 5 OK.

2. n·q ≥ 5 → 1000·(1-0.2) = 800 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

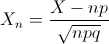
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(20, √19.6).

Debemos obtener la siguiente probabilidad:

P(X ≥ 27) = 1 - P(X < .27)

Aplicamos el factor de corrección:

P(X ≥ 26) = 1 - P(X < .26.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

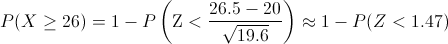
Obtenemos:

P(X ≥ 26) = 1 - P(Z < .1.47) = 1 - [0.5 + Φ(1.47)] = 0.5 - Φ(1.47)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X ≥ 26) = 0.5 - Φ(1.47) = 0.5 - 0.4292 = 0.0708

Por lo tanto, la probabilidad de que 27 o más fusibles sean defectuosos de una muestra de 1000, es de 0.0708.