Problema44: VAC

Ej44. El volumen que una máquina de llenado automático deposita en latas de una bebida gaseosa tiene una distribución normal con media 34 cl. y una desviación típica 1,5 cl.

Determinar:

a) Si se despachan aquellas latas que tienen menos de 33 cl., ¿cuál es la probabilidad de latas desechadas?.

b) La máquina de llenado puede ser ajustada para cambiar el volumen medio, obtener dicho volumen medio para que únicamente el 1% de las latas tuviera menos de 33 cl.

c) Si tomamos 500 latas llenadas con la máquina tal y como figura originalmente, ¿cuál es la probabilidad de que al menos 100 sean desechadas?.


Sea la variable aleatoria X, número de latas desechadas. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.

Cuya media es: 34 y la desviación estándar: 1.5.

Pasamos a resolver los distintos apartados ofrecidos.


Apartado a)

Debemos obtener la siguiente probabilidad:

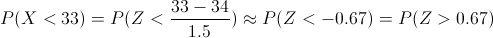
Operamos:

P(X < .33) ≈ 1- P(Z ≤ 0.67) = 1-(0.5+Φ(0.67)) = 0.5 - Φ(0.67)

Buscamos en las tablas de la Normal expuestas en este blog, para dar cómo resultado final:

P(X < .33) ≈ 1- P(Z ≤ 0.67) = 0.5 - 0.2486 = 0.2514

Por lo tanto, la probabilidad de que las latas sean desechadas es de 0.2514.


Apartado b)

En este apartado, nos dan los datos de la probabilidad y debemos hallar el valor de la media que lo satisfaga.

Tenemos: P(X < .33) = 0.01

Tipificamos:

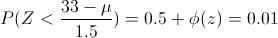
Despejamos:

Φ(z) = 0.01 - 0.5 = -0.49

El valor es negativo, esto nos indica que la probabilidad se encuentra en el lado derecho de la Campana de Gauss. Dicha causa no nos impide obtener un valor, ya que la curva es simétrica.

Buscamos en las tablas de la Normal el valor 0.49, pero en este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..2.33.............Z..........2.34
0.4898........0.49.....0.4901

De donde:

0.4898 - 0.4901.-> 2.33 - 2.34
0.4898 - 0.49..-> 2.33 - Z

Calculamos:

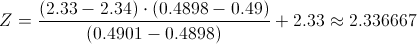
Teniendo en cuenta que el valor se encuentra en la parte izquierda de la curva, tenemos que otorgarle el signo negativo:

· Z = -2.336667

Por lo tanto, la nueva media será:

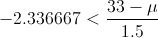
Despejamos μ:

μ < .36.505001

Por lo tanto, el volumen medio que satisface los condicionantes que nos propone este apartado es de, aproximadamente, μ < .36.505001 cl.


Apartado c)

Sea la variable aleatoria discreta X, número de latas desechadas. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:

La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(500, 0.2514).

NOTA: La probabilidad de que una lata sea desechada se ha obtenido en el Apartado a).

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 500·0.2514 = 125.7 ≥ 5 OK.

2. n·q ≥ 5 → 500·(1-0.2514) = 94.09902 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

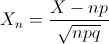
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(125.7, √94.09902).

En este apartado debemos obtener la siguiente probabilidad:

P(X ≥ 100) = 1 - P(X < .100)

Aplicamos el factor de corrección:

P(X ≥ 100) = 1 - P(X < .95.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

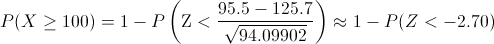
Obtenemos:

P(X ≥ 100) = 1 - [1 - P(Z ≤ 2.70)] = P(Z ≤ 2.70) = 0.5 + Φ(2.70)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X ≥ 100) = 0.5 + Φ(2.70) = 0.5 + 0.4965 = 0.9965

Por lo tanto, si tomamos 500 de estas latas, la probabilidad de que al menos 100 se desechen, es de 0.9965, una probabilidad alta.