Ej21. A fin de estudiar la evolución del ángulo de Clarke (en grados) con la edad del niño (sano) se obtuvieron ambos datos en un grupo de 16 niños (entre 3 y 10 años) elegidos al azar:Edad(X).. 3. 3. 4. 4. 5. 5. 6. 6. 7. 7 8... 8... 9... 9... 10... 10 Ángulo(y) 24 22 28 25 32 31 33 30 34 34 36 39 39 41 46 44
a) Encuentra la recta de regresión que relaciona ambas variables.
b) ¿Existe relación entre la edad y el ángulo de Clarke?.
c) ¿Qué porcentaje de la variabilidad del ángulo queda explicada por la relación que mantiene con la variable edad?.
d) ¿Qué valor del ángulo tendrá un niño con 12 años?¿Y uno de 5 años?.
Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.
· n = 16
· 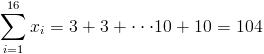
· 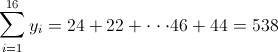
· 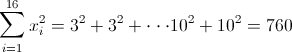
· 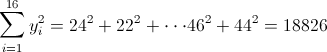
· 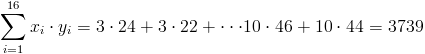
Apartado a)
Para calcular la pendiente, la expresión matemática es:
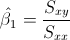
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:
·
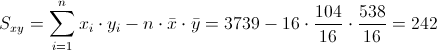
·
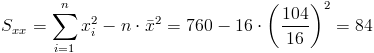
Por lo tanto, la pendiente es:
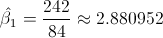
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:
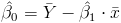
Sustituimos valores:
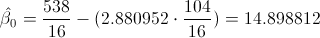
Por lo tanto, la ecuación de regresión ajustada es:
· y ≡ Ángulo de Clarke.
· x ≡ Edad de niño sano.
Apartado b)
Para comprobar si existe relación entre variables, obtenemos el coeficiente de correlación, empleamos su expresión matemática:
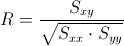
Debemos obtener Syy:
·
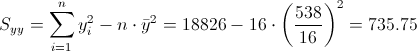
Sustituimos valores y obtenemos el resultado del coeficiente de correlación:
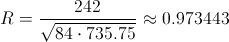
Por lo tanto, al estar próximo a 1 el valor del coeficiente de correlación, podemos afirmar que existen evidencias significativas de que ambas variables estén relacionadas.
Apartado c)
Para obtener la variabilidad, obtenemos el coeficiente de determinación, empleamos su expresión matemática:
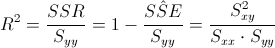
Sustituimos valores y obtenemos el resultado del coeficiente de correlación:
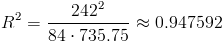
Por lo tanto, el porcentaje de variabilidad es de, aproximadamente 94.76%.
Apartado d)
Para obtener los valores del ángulo, emplearemos la recta ajustada:
· Para un niño sano de 12 años.
Para este caso, no sería fiable obtener tal ángulo ya que al determinar la recta de regresión, el límite máximo es de 10 años.
· Para un niño sano de 5 años.
Empleamos la recta ajustada:
Por lo tanto, para un niño sano de 5 años, el ángulo según la recta ajustada es de, aproximadamente 29.





2 comentarios:
estimado tengo un problema que no se como resolver
los pesos de los cerdos tienen una distrib.normal media mu y varianza sigma cuadrado.
se toma muestra aleatoria de 9 cerdos
1)determine mu si se sabe que sigma cuadrado=36 y que P(X barra < o igual que 92)=0.0668
porfavor,cualquier ayuda se agradeceria mucho
mi mail es alejandra.sotogrez@gmail.com
Buenas Alejandra:
Primero, aconsejarte que las preguntas que sean de variables continuas vayan en la sección correspondiente, ya que en este caso, este problema es de regresión lineal. Te digo esto para mantener un orden lógico.
Por otro lado, el problema que mencionas lo podrás encontrar en la sección que te he mencionado anteriormente, no el mismo pero sí similares, aún así y sin servir de precedente, te lo resolveré:
Datos:
· X ≡ 'Peso de los cerdos'
· Muestra de 9 cerdos.
· X ~ N(9μ, 6·√9) = N(9μ, 18)
Debemos resolver:
P(X ≤ 92) = 0.0668
Tipificamos:
P(Z ≤ (92-9μ)/18) = 0.5+Φ(z) = 0.0668
Despejamos:
Φ(z) = 0.0668-0.5 = -0.4332
Buscamos en las tablas de la Normal, el signo negativo no nos incomoda ya que sabemos que la curva es simétrica: Φ(z) = -1.50
Por lo tanto:
-1.50 ≤ (92-9μ)/18
Despejamos μ para obtener la solución a este problema:
· μ ≤ 13.222222
· PD: Recordarte lo de preguntar cada cosa en el apartado correspondiente.
· PPDD: Mírate los ejercicios resueltos que te serán de gran ayuda y te resolverán la mayoría de los problemas que te puedas plantear.
Un saludo y gracias por tu comentario.
Publicar un comentario