Problema64: Probabilidad

Ej64. Supongamos que un dormitorio estudiantil en una universidad está conformado por:

· 30% de estudiantes de primer año, de los cuales el 10% poseen un auto.
· 40% de estudiantes de segundo año, de los cuales el 20% poseen un auto.
· 20% de estudiantes de tercer año, de los cuales el 40% poseen un auto.
· 10% de estudiantes de cuarto año, de los cuales el 60% poseen un auto.

Determinar:

a) Encuentre la probabilidad de que un estudiante en el dormitorio posea un auto.

b) Si un estudiante posee un auto, encuentre la probabilidad de que el estudiante sea de tercer año.


Realizamos una recopilación de datos dados por el enunciado del problema:

· A ≡ 'Estudiante del 1º año'.
· B ≡ 'Estudiante del 2º año'.
· C ≡ 'Estudiante del 3º año'.
· D ≡ 'Estudiante del 4º año'.

· P(A) = 0.3.
· P(B) = 0.4.
· P(C) = 0.2.
· P(D) = 0.1.

· M ≡ 'Tener auto'.

· P(M|A) = 0.1.
· P(M|B) = 0.2.
· P(M|C) = 0.4.
· P(M|D) = 0.6.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de tener auto, para ello, empleamos la Probabilidad Total:

P(M) = P(M|A)·P(A) + P(M|B)·P(B) + P(M|C)·P(C) + P(M|D)·P(D)

Sustituimos valores para obtener la solución a este apartado:

P(M) = 0.1·0.3 + 0.2·0.4 + 0.4·0.2 + 0.6·0.1 = 0.25

Por lo tanto, la probabilidad de tener auto es de 0.25.


Apartado b)

En este apartado nos piden obtener la probabilidad de que dado que tenga auto, sea de un estudiante del tercer año:

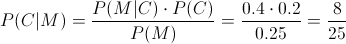
Por lo tanto, la probabilidad de que dado que un alumno tenga auto, sea del tercer año es de 0.32.