Problema65: Probabilidad

Ej65. Una caja contiene 10 monedas, donde hay 5 monedas de dos caras, 3 monedas tienen dos sellos y 2 monedas son corrientes.

Se selecciona una moneda al azar y se lanza, determinar:

a) La probabilidad de que aparezca una cara.

b) Si aparece una cara, encuentre la probabilidad de que la moneda sea corriente.


Realizamos una recopilación de datos dados por el enunciado del problema:

· A ≡ 'Moneda de dos caras'. Monedas: 5.
· B ≡ 'Moneda de dos sellos'. Monedas: 3.
· D ≡ 'Moneda normal: una cara y un sello'. Monedas: 2.

Número total de monedas: 5+3+2 = 10 monedas.

· P(A) = 5/10 = 1/2.
· P(B) = 3/10.
· P(D) = 2/10 = 1/5.

· C ≡ 'Cara de la moneda'.

· P(C|A) = 1.
· P(C|B) = 0.
· P(C|D) = 0.5.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de salir cara al lanzar una moneda escogida al azar entre las dadas, para ello, empleamos la Probabilidad Total:

P(C) = P(C|A)·P(A) + P(C|B)·P(B) + P(C|D)·P(D)

Sustituimos valores para obtener la solución a este apartado:

P(C) = 1·(1/2) + 0·(3/10) + 0.5·(2/10) = 3/5

Por lo tanto, la probabilidad de obtener cara es de 0.6.


Apartado b)

En este apartado nos piden obtener la probabilidad de que dado que salga cara, sea de la moneda normal:

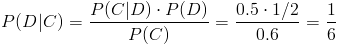
Por lo tanto, la probabilidad de que dado que salga cara, sea de la moneda normal es de, aproximadamente 0.166667.