Problema72: Probabilidad

Ej72. En una población de moscas de fruta el 25% presentan una mutación en los ojos, el 50% presentan mutación en las alas y el 40% de las que presentan mutación en los ojos presentan mutación en las alas.

Se elige una mosca al azar:

a) ¿Cuál es la probabilidad de que la mosca presente al menos una de las mutaciones?

b) Si tiene mutación en las alas, ¿cuál es la probabilidad de que no presente mutación en los ojos?

c) ¿Cuál es la probabilidad de que la mosca presente mutación en los ojos pero no en las alas?


Realizamos una recopilación de datos dados por el enunciado del problema:

· E ≡ 'Mutación en los ojos'.
· O ≡ 'Mutación en las alas'.

· P(E) = 0.25.
· P(O) = 0.5.
· P(O|E) = 0.4.

Hay que tener en cuenta que por los datos ofrecidos por el enunciado, ambos eventos no son mutuamente excluyentes.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que al escoger una mosca al azar, presente alguna de las mutaciones:

P(EUO) = P(E) + P(O) - P(E∩O) = P(E) + P(O) - P(O|E)·P(E) = 0.25 + 0.5 - 0.4·0.25 = 0.65

Por lo tanto, la probabilidad de que la mosca padezca alguna de las mutaciones es de 0.65.


Apartado b)

En este apartado nos piden obtener la probabilidad de que teniendo mutación en las alas, no presente mutación en los ojos:

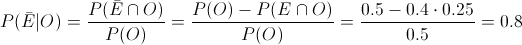
Por lo tanto, la probabilidad de que teniendo mutación en las alas, no presente mutación en los ojos es de 0.8.


Apartado c)

En este apartado nos piden obtener la probabilidad de que la mosca presente mutaciones en los ojos pero no en las alas:

P(E∩Ō) = P[E∩(1-O)] = P(E) - P(E∩O) = P(E) - P(O|E)·P(E) = 0.25 - 0.4·0.25 = 0.15

Por lo tanto, la probabilidad de que la mosca presente mutaciones en los ojos pero no en las alas es de 0.15.