Ej29. Suponga que el gerente de una cadena de servicios de entrega de paquetería desea desarrollar un modelo para predecir las ventas semanales (en miles de dólares) para las tiendas individuales basado en el número de clientes que realizan compras.
Se seleccionó una muestra aleatoria entre todas las tiendas de la cadena con los siguientes resultados:Clientes 907 926 506 741 789 889 874 510 529 420 Ventas 11.2. .11.05. .6.84. .9.21. .9.42. .10.08. .9.45. .6.73. .7.24. .6.12.
Obtener:
a) Encuentra la recta de regresión que relaciona ambas variables.
b) Pronostique las ventas semanales para las tiendas que tienen 600 clientes.
c) Calcule el coeficiente de determinación e interprete su significado.
Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.
· n = 10
· 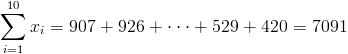
· 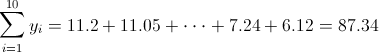
· 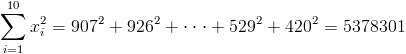
· 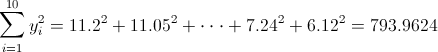
· 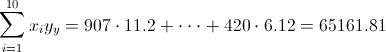
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Para calcular la pendiente, la expresión matemática es:
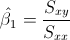
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:
·
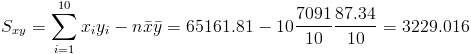
·
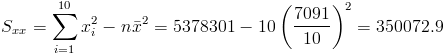
Por lo tanto, la pendiente es:
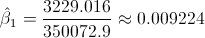
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:
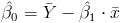
Sustituimos valores:
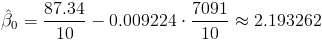
Por lo tanto, la ecuación de regresión ajustada es:
Apartado b)
En este apartado, debemos obtener el valor mediante la recta ajustada.
· Para Número de Clientes = 600:
Por lo tanto, para un número de 600 clientes se pronostica que se generen, aproximadamente, 7.73 miles de dólares.
Apartado c)
Para obtener el coeficiente de determinación, empleamos su expresión matemática:
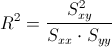
Debemos obtener el valor de Syy:
·
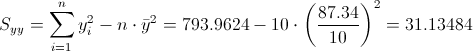
Sustituimos valores y obtenemos el resultado del coeficiente de determinación:
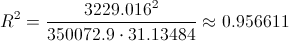
Por lo tanto, el porcentaje de variabilidad es de, aproximadamente 95.66%, esto quiere decir que el 95.66% de la variación en las ventas se explica por la variación en el número de clientes.





0 comentarios:
Publicar un comentario