Problema30: Análisis de Regresión

Ej30. Un profesor de Estadística realiza un examen final y exige también a los estudiantes que realicen un proyecto de análisis de datos. Las calificaciones obtenidas por una muestra aleatoria aparecen en la siguiente tabla:

Examen	81	62	74	78	93	69	72	83	90	84
Proyecto	76.	.71.	.69.	.76.	.87.	.62.	.80.	.75.	.92.	.79.

Siendo:

· X ≡ Examen.
· Y ≡ Proyecto

Obtener:

a) Encuentra la recta de regresión que relaciona ambas variables.

b) Calcule el coeficiente de determinación e interprete su significado.

c) ¿Qué nota cree usted que sacaría un alumno que tuvo 75 en el examen?.

d) Si un alumno tiene 75 en el examen, obtener un intervalo de confianza para la respuesta media al 90%.

e) Si un alumno tiene 75 en el examen, obtener un intervalo de predicción para observaciones futuras al 90%.


Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.

· n = 10

·

·

·

·

·

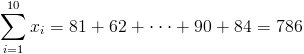
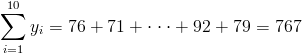
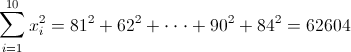
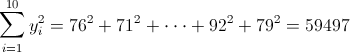
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Para calcular la pendiente, la expresión matemática es:

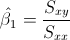
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·

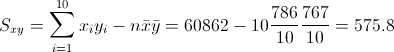
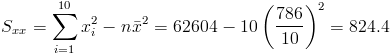
Por lo tanto, la pendiente es:

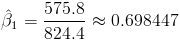
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:

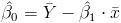
Sustituimos valores:

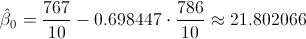
Por lo tanto, la ecuación de regresión ajustada es:

y(x) = 21.802066 + 0.698447·x

Apartado b)

Para obtener el coeficiente de determinación, empleamos su expresión matemática:

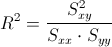
Debemos obtener el valor de Syy:

·

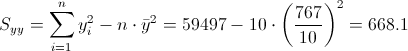
Sustituimos valores y obtenemos el resultado del coeficiente de determinación:

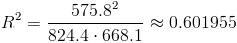
Por lo tanto, el porcentaje de variabilidad es de, aproximadamente 60.20%, esto quiere decir que el 60.20% de la variación en las notas del examen se explica por la variación en las notas del proyecto.


Apartado c)

En este apartado, debemos obtener el valor mediante la recta ajustada.

y(x) = 21.802066 + 0.698447·x

· Para Nota del Examen = 75:

y(75) = 21.802066 + 0.698447·75 = 74.185591

Por lo tanto, para una nota del examen de 75 puntos se pronostica que se obtenga en el proyecto un total de 74.185591 puntos.


Apartado d)

En este apartado nos piden obtener un intervalo para la respuesta media, cuya expresión matemática es:

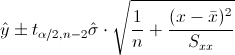
Al 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.1/2, 10-2} = t_{0.05, 8} = 1.8595

Debemos obtener el valor del estimador de la desviación estándar:

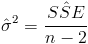
Siendo:

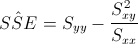
Disponemos de todos los datos necesarios para estimar la varianza:

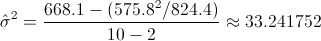
El único dato que nos falta por obtener es el valor del parámetro Y cuando x vale 75, para ello, usamos la recta ajustada calculada en el Apartado c):

· y(75) = 21.802066 + 0.698447·75 = 74.185591.

Sustituimos valores en la expresión del intervalo de confianza para la respuesta media

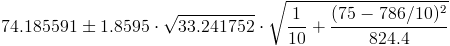
Por lo tanto, el intervalo de confianza para la respuesta media al 90% es,aproximadamente:

[70.538527, 77.832655]

Apartado e)

En este apartado nos piden obtener un intervalo de predicción para observaciones futuras, cuya expresión matemática es:

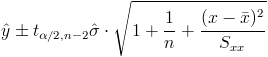
Al 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.1/2, 10-2} = t_{0.05, 8} = 1.8595

El único dato que nos falta por obtener es el valor del parámetro Y cuando x vale 75, para ello, usamos la recta ajustada calculada en el Apartado c):

· y(75) = 21.802066 + 0.698447·75 = 74.185591.

Sustituimos valores en la expresión del intervalo de predicción para observaciones futuras:

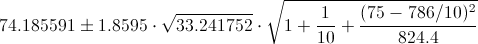
Por lo tanto, el intervalo de predicción al 90% es,aproximadamente:

[62.861174, 85.510008]