Ej2. En el siguiente recuadro, se relacionan en pulgadas (x 0.001), los diámetros de una muestra de 60 cojinetes fabricados por Hades.
Agrúpelos en seis clases. Calcule las frecuencias absolutas, los representantes de clase, la media y la mediana, tanto en los datos agrupados como sin agrupar.
| 724 | 725 | 726 | 727 | 727 | 728 | 728 | 729 | 729 | 730 | 730 | 730 | 731 | 731 |
| 732 | 732 | 732 | 732 | 732 | 733 | 733 | 733 | 734 | 734 | 734 | 734 | 735 | 735 |
| 735 | 735 | 735 | 735 | 735 | 735 | 736 | 736 | 736 | 736 | 736 | 736 | 737 | 737 |
| 737 | 738 | 738 | 738 | 739 | 739 | 739 | 740 | 740 | 740 | 741 | 741 | 742 | 742 |
| 743 | 744 | 745 | 746 |
· Sugerencia: Para facilitar el agrupamiento en seis clases, amplíe ligeramente el intervalo que contiene los datos, tomando como extremo izquierdo del mismo, 723 y como extremo derecho 747.
Lo primero que debemos hacer, es trabajar con datos más flexibles, por lo tanto, ampliamos el intervalo en los límites del mismo.
· b = 747
Tomamos las clases que nos indica el enunciado: p = 6.
Una vez dispuesto los límites del intervalo, calculamos la longitud:
No hace falta redondear el valor de h ya que es igual al número de cifras decimales que poseen los datos de la muestra, por lo tanto:
· d = 0
En estos momentos, se está listo para realizar los intervalos y las marcas del mismo:
· Primer Intervalo.
Subintervalo Inferior: e1 = a = 723
Subintervalo Superior: e2 = a + h - 10-d = 723 + 4 - 10-0 = 726
Marca: x1 = (e1 + e2)/2 = (723 + 726)/2 = 724.5
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 723 + 4 = 727
Subintervalo Superior: e3 = a + 2h - 10-d = 723 + 2·4 - 10-0 = 730
Marca: x2 = (e2 + e3)/2 = (727 + 730)/2 = 728.5
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 723 + 2·4 = 731
Subintervalo Superior: e4 = a + 3h - 10-d = 723 + 3·4 - 10-0 = 734
Marca: x3 = (e3 + e4)/2 = (731 + 734)/2 = 736.5
Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 723 + 3·4 = 735
Subintervalo Superior: e5 = a + 4h - 10-d = 723 + 4·4 - 10-0 = 738
Marca: x4 = (e4 + e5)/2 = (735 + 738)/2 = 736.5
Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 723 + 4·4 = 739
Subintervalo Superior: e6 = a + 5h - 10-d = 723 + 5·4 - 10-0 = 742
Marca: x5 = (e5 + e6)/2 = (739 + 742)/2 = 740.5
Sexto Intervalo.
Subintervalo Inferior: e6 = a + 5h = 723 + 5·4 = 743
Subintervalo Superior: e7 = a + 6h - 10-d = 723 + 6·4 - 10-0 = 742
Marca: x6 = (e6 + e7)/2 = (743 + 742)/2 = 744.5
La frecuencia absoluta será el número de veces que aparecen datos en los respectivos intervalos calculados anteriormente.
Para ello, empezamos a contar cuantos datos están dentro de cada intervalo de la tabla de datos original del problema, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi |
| 723 – 726 | 724.5 | 3 |
| 727 – 730 | 728.5 | 9 |
| 731 – 734 | 732.5 | 14 |
| 735 – 738 | 736.5 | 20 |
| 739 – 742 | 740.5 | 10 |
| 743 – 746 | 744.5 | 4 |
Se puede observar, que las clases construidas de la manera que se ha descrito con anterioridad, están separadas unas de otras, es decir, entre una clase y la siguiente hay un espacio que no pertenece a ninguna de las dos, en el que no hay (precisamente se ha construido así) ningún dato.
Vamos a realizar una pequeña modificación para evitar dicha separación entre clases pero manteniendo el hecho de que cada dato pertenezca a una y sólo una clase.
La metodología consiste en dividir por la mitad el espacio entre cada dos clases consecutivas, y tomar así, el punto medio como extremo superior para una clase e inferior para la siguiente.
Dado que la longitud de este espacio entre clases es 10-d, la mitad será 0.5·10-d.
Aplicando lo anterior, los extremos de las clases quedan de la siguiente manera:
· Primer Intervalo.
Subintervalo Inferior: e1 = a = 723
Subintervalo Superior: e2 = a + h - 0.5·10-d = 723 + 4 - 0.5·10-0 = 726.5
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 723 + 4 = 727
Subintervalo Superior: e3 = a + 2h - 0.5·10-d = 723 + 2·4 - 0.5·10-0 = 730.5
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 723 + 2·4 = 731
Subintervalo Superior: e4 = a + 3h - 0.5·10-d = 723 + 3·4 - 0.5·10-0 = 734.5
· Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 723 + 3·4 = 735
Subintervalo Superior: e5 = a + 4h - 0.5·10-d = 723 + 4·4 - 0.5·10-0 = 738.5
· Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 723 + 4·4 = 739
Subintervalo Superior: e6 = a + 5h - 0.5·10-d = 723 + 5·4 - 0.5·10-0 = 742.5
· Sexto Intervalo.
Subintervalo Inferior: e6 = a + 5h = 723 + 5·4 = 743
Subintervalo Superior: e7 = a + 6h - 0.5·10-d = 723 + 6·4 - 0.5·10-0 = 742.5
Por su puesto, las marcas siguen siendo de igual valor, por lo tanto, la tabla definitiva queda de la siguiente manera:
| Subintervalos | Marca |
| 722.5 – 726.5 | 724.5 |
| 726.5 – 730.5 | 728.5 |
| 730.5 – 734.5 | 732.5 |
| 734.5 – 738.5 | 736.5 |
| 738.5 – 742.5 | 740.5 |
| 742.5 – 746.5 | 744.5 |
Hay que decir, que los intervalos sin espacios no es necesario calcularlo ya que no lo pide el enunciado, pero se exponen ya que no es una técnica difícil.
Una vez obtenidos los datos agrupados, nos piden calcular la media y la mediana tanto para los datos agrupados como para los datos originales sin agrupar.
Por lo tanto, dividiremos el problema en dos, por una parte los datos originales sin agrupar y por otra los datos agrupados.
Para ambos, el número total de datos es N = 60.
Datos sin Agrupar.
La expresión de la media es la que se muestra a continuación:
La expresión de la mediana es la siguiente:
- Si N es impar:
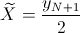
Si N es par:
La media es:
La mediana, teniendo en cuenta que N es un número par, será:
Datos Agrupados.
La media para datos agrupados se calcula mediante la siguiente expresión:
Para la mediana, es preciso localizar aquella clase que cumple las desigualdades siguientes:
· Fk > N/2
· Fk-1 < N/2
Con las expresiones y consideraciones anteriores, calculamos lo que nos piden.
La media es:
Para hallar este apartado, necesitamos calcular la frecuencia absoluta acumulada.
Las frecuencias absolutas acumuladas se obtienen aplicando la siguiente expresión:
Es decir, la frecuencia absoluta acumulada del primer subintervalo será igual a su frecuencia absoluta.
En cambio, la frecuencia absoluta acumulada del segundo subintervalo, será la suma de la frecuencia absoluta del intervalo anterior más la frecuencia absoluta suya.
Y así será la forma de proceder, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi |
| 723 – 726 | 724.5 | 3 | 3 |
| 727 – 730 | 728.5 | 9 | 12 |
| 731 – 734 | 732.5 | 14 | 26 |
| 735 – 738 | 736.5 | 20 | 46 |
| 739 – 742 | 740.5 | 10 | 56 |
| 743 – 746 | 744.5 | 4 | 60 |
Para la mediana, es preciso localizar aquella clase que cumple las desigualdades anteriormente mencionadas.
La clase que cumple dicha desigualdad, es la del subintervalo 731 – 734 con una frecuencia absoluta acumulativa de F = 26 y el subintervalo 735 – 738 con una frecuencia absoluta de f = 20 y una frecuencia absoluta acumulativa de F = 46.
Y la expresión de la mediana para datos agrupados es la siguiente:

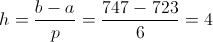
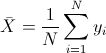

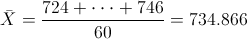

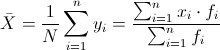
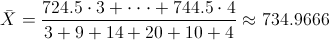
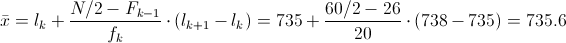




4 comentarios:
ey! esta genial esto del blog explicandonos esto, pero hay muchos fallos en los problemas. Fallos en las operaciones, no en las explicaciones. Supongo que te interesara. Gracias x el blog.
Buenas:
Gracias por tu comentario, con respecto a los fallos, todos somos humanos y seguramente algunos habrá, ya que escribir en LaTeX con blogger es algo tedioso.
En todo caso, díctame los errores que encuentres para poder subsanarlos.
Gracias.
Gracias por el blog,es genial! Mi duda es: porque amplia un numero por debajo y otro por encima para facilitar el agrupamiento en seis clases?no lo entiendo.gracias.
Buenas:
Se amplia simplemente para facilitar los cálculos posteriores que serán necesarios a la hora de resolver el problema, es más, dicha ampliación del intervalo es un dato del problema, no algo que hagamos por que queramos.
Como curiosidad, puedes hacerlo de ambas maneras, una teniendo en cuenta la sugerencia del enunciado del problema, y otra, sin tenerla en cuenta.
Y descubres si es cierto que teniendo dicha sugerencia del enunciado es más fácil o no.
Un saludo.
Publicar un comentario