Ej3. Los datos numéricos que siguen son las clasificaciones obtenidas por 80 personas a las que se ha sometido a cierta prueba.
Calcule la media, la mediana y cuasi desviación típica, agrupándolos previamente. Los datos en cinco clases.
| 53 | 57 | 59 | 60 | 60 | 60 | 61 | 61 | 62 | 62 | 62 | 62 | 63 | 63 | 65 | 65 | 65 |
| 66 | 67 | 67 | 68 | 68 | 68 | 69 | 71 | 71 | 71 | 72 | 72 | 73 | 73 | 73 | 73 | 74 |
| 74 | 74 | 75 | 75 | 75 | 75 | 75 | 75 | 75 | 76 | 76 | 76 | 76 | 77 | 77 | 78 | 78 |
| 78 | 78 | 78 | 79 | 79 | 79 | 80 | 81 | 82 | 82 | 83 | 84 | 85 | 85 | 85 | 86 | 87 |
| 88 | 88 | 88 | 89 | 90 | 93 | 93 | 94 | 95 | 95 | 96 |
· Sugerencia: Para facilitar el agrupamiento en cinco clases, amplíe el intervalo a [53, 97] que contiene los datos originales al intervalo [50, 100].
El enunciado nos indica que ampliemos el intervalo ligeramente, por lo tanto, los límites quedan definidos de la siguiente manera:
· b = 100
Tomamos las clases que nos indica el enunciado: p = 5.
Una vez dispuesto los límites del intervalo, calculamos la longitud:
No hace falta redondear el valor de h ya que es igual al número de cifras decimales que poseen los datos de la muestra, por lo tanto,
Y ya se está listo para realizar los intervalos y las marcas del mismo:
Primer Intervalo.
Subintervalo Inferior: e1 = a = 50
Subintervalo Superior: e2 = a + h - 10-d = 50 + 10 - 10-0 = 59
Marca: x1 = (e1 + e2)/2 = (50 + 59)/2 = 54.5
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 50 + 10 = 60
Subintervalo Superior: e3 = a + 2h - 10-d = 50 + 2·10 - 10-0 = 69
Marca: x2 = (e2 + e3)/2 = (60 + 69)/2 = 64.5
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 50 + 2·10 = 70
Subintervalo Superior: e4 = a + 3h - 10-d = 50 + 3·10 - 10-0 = 79
Marca: x3 = (e3 + e4)/2 = (70 + 79)/2 = 74.5
Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 50 + 3·10 = 80
Subintervalo Superior: e5 = a + 4h - 10-d = 50 + 4·10 - 10-0 = 89
Marca: x4 = (e4 + e5)/2 = (80 + 89)/2 = 84.5
Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 50 + 4·10 = 90
Subintervalo Superior: e6 = a + 5h - 10-d = 50 + 5·10 - 10-0 = 99
Marca: x5 = (e5 + e6)/2 = (90 + 99)/2 = 94.5
Para hallar la media, la mediana y la cuasi desviación típica, es conveniente obtener las frecuencias absolutas (fi) y las frecuencias absolutas acumulativas (Fi).
La frecuencia absoluta será el número de veces que aparecen datos en los respectivos intervalos calculados anteriormente.
Para ello, empezamos a contar cuantos datos están dentro de cada intervalo de la tabla de datos original del problema, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi |
| 50 – 59 | 54.5 | 3 |
| 60 – 69 | 64.5 | 21 |
| 70 – 79 | 74.5 | 33 |
| 80 – 89 | 84.5 | 15 |
| 90 – 99 | 94.5 | 8 |
Una vez obtenidas las frecuencias absolutas, se obtienen las frecuencias absolutas acumuladas.
Las frecuencias absolutas acumuladas se obtienen aplicando la siguiente expresión:
Es decir, la frecuencia absoluta acumulada del primer subintervalo será igual a su frecuencia absoluta.
En cambio, la frecuencia absoluta acumulada del segundo subintervalo, será la suma de la frecuencia absoluta del intervalo anterior más la frecuencia absoluta suya.
Y así será la forma de proceder, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulativa, Fi |
| 50 – 59 | 54.5 | 3 | 3 |
| 60 – 69 | 64.5 | 21 | 24 |
| 70 – 79 | 74.5 | 33 | 57 |
| 80 – 89 | 84.5 | 15 | 72 |
| 90 – 99 | 94.5 | 8 | 80 |
Se puede observar, que las clases construidas de la manera que se ha descrito con anterioridad, están separadas unas de otras, es decir, entre una clase y la siguiente hay un espacio que no pertenece a ninguna de las dos, en el que no hay (precisamente se ha construido así) ningún dato.
Vamos a realizar una pequeña modificación para evitar dicha separación entre clases pero manteniendo el hecho de que cada dato pertenezca a una y sólo una clase.
La metodología consiste en dividir por la mitad el espacio entre cada dos clases consecutivas, y tomar así, el punto medio como extremo superior para una clase e inferior para la siguiente.
Dado que la longitud de este espacio entre clases es 10-d, la mitad será 0.5·10-d.
Aplicando lo anterior, los extremos de las clases quedan de la siguiente manera:
· Primer Intervalo.
Subintervalo Inferior: e1 = a = 50
Subintervalo Superior: e2 = a + h - 0.5·10-d = 50 + 10 - 0.5·10-0 = 59.5
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 50 + 10 = 60
Subintervalo Superior: e3 = a + 2h - 0.5·10-d = 50 + 2·10 - 0.5·10-0 = 69.5
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 50 + 2·10 = 70
Subintervalo Superior: e4 = a + 3h - 0.5·10-d = 50 + 3·10 - 0.5·10-0 = 79.5
· Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 50 + 3·10 = 80
Subintervalo Superior: e5 = a + 4h - 0.5·10-d = 50 + 4·10 - 0.5·10-0 = 89.5
· Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 50 + 4·10 = 90
Por su puesto, las marcas siguen siendo de igual valor, por lo tanto, la tabla definitiva queda de la siguiente manera:
| Subintervalos | Marca |
|
49.5 – 59.5 | 54.5 |
|
59.5 – 69.5 | 64.5 |
|
69.5 – 79.5 | 74.5 |
|
79.5 – 89.5 | 84.5 |
|
89.5 – 99.5 | 94.5 |
Hay que decir, que los intervalos sin espacios no es necesario calcularlo ya que no lo pide el enunciado, pero se exponen ya que no es una técnica difícil.
Una vez obtenidos los datos agrupados, nos piden calcular la media, la mediana y la cuasi desviación típica.
El número total de datos es N = 80.
· Datos Agrupados.
La media para datos agrupados se calcula mediante la siguiente expresión:
Calculamos lo que nos piden. La media es:
· Fk > N/2
· Fk-1 < N/2
La clase que cumple dicha desigualdad, es la del subintervalo, Fk, 70 – 79 con una frecuencia absoluta de f = 33 y el subintervalo, Fk-1, 60 – 69, con una frecuencia absoluta acumulativa de Fk = 24.
Y la expresión de la mediana para datos agrupados es la siguiente:
Lo último que nos queda por calcular, es la cuasi desviación típica, para ello aplicamos la expresión siguiente para su cálculo:
Se obtiene:

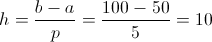
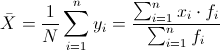

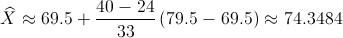






6 comentarios:
Creo que el enunciado esta equivocado, pues solo cuento 79 datos
Buenas:
Si te das cuenta, en el enunciado te aconsejan que se amplíe el intervalo a [53, 97].
Y es ese precisamente 97, el que hace que sean en total 80 datos.
Un saludo.
Lo que no entiendo es porque se aconseja que se amplie un dato mas.¿porque no hacerlo con 79 datos?
Buenas:
Generalmente se suele hacer para facilitar los cálculos. Es por ello, que es en el enunciado donde se indica que se amplíe el intervalo.
En caso de que el enunciado no mencione nada, pues no se amplia.
Un saludo.
lo que no entiendo es porque amplia hasta el 100 y el 50,en otros problemas se amplia solo una unidad por debajo y otra por arriba.Gracias!
Buenas:
Se amplía simplemente para facilitar los cálculos numéricos, es más, es una sugerencia del enunciado del problema por lo tanto, no tiene mucha más ciencia.
Al ser algo que te dice el enunciado se hace sin más, en este caso concreto, es una sugerencia, por lo tanto, de ti depende si quieres seguirla o no.
Como curiosidad, puedes realizar este problema tomando la sugerencia y después sin hacerle caso a la sugerencia, a ver si es más complicado o no.
Un saludo.
Publicar un comentario