Ej4. Se dispone de la medida en milímetros de los diámetros (x 0.01) de 40 bolas, relacionadas en la tabla que sigue a continuación.
| 840 | 840 | 841 | 841 | 842 | 843 | 843 | 845 | 846 | 846 | 847 | 847 | 850 | 851 |
| 851 | 852 | 852 | 853 | 853 | 854 | 854 | 854 | 855 | 855 | 856 | 856 | 856 | 857 |
| 857 | 859 | 859 | 859 | 860 | 860 | 861 | 861 | 862 | 863 | 868 | 868 |
Construya la distribución de frecuencias, y halle la media, la mediana y la cuasi desviación típica de dos maneras:
a) Agrupando los datos en seis clases. Para ello, amplíe el intervalo que contiene los datos hasta el [840, 870].
b) Agrupando los datos en siete clases sin ampliar el intervalo (observe que la última clase ha de ser algo mayor que las demás)
Apartado a)
El enunciado nos indica que ampliemos el
intervalo ligeramente, por lo tanto, los límites quedan definidos de la
siguiente manera:
· b = 870
Tomamos las clases que nos indica el enunciado: p = 6.
Una vez dispuesto los límites del intervalo, calculamos la longitud:
No hace falta redondear el valor de h ya que es igual al número de cifras decimales que poseen los datos de la muestra, por lo tanto,
· d = 0
Primer Intervalo.
Subintervalo Inferior: e1 = a = 840
Subintervalo Superior: e2 = a + h - 10-d = 840 + 5 - 10-0 = 844
Marca: x1 = (e1 + e2)/2 = (840 + 844)/2 = 842
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 840 + 5 = 845
Subintervalo Superior: e3 = a + 2h - 10-d = 840 + 2·5 - 10-0 = 849
Marca: x2 = (e2 + e3)/2 = (845 + 849)/2 = 847
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 840 + 2·5 = 850
Subintervalo Superior: e4 = a + 3h - 10-d = 840 + 3·5 - 10-0 = 854
Marca: x3 = (e3 + e4)/2 = (850 + 854)/2 = 852
Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 840 + 3·5 = 855
Subintervalo Superior: e5 = a + 4h - 10-d = 840 + 4·5 - 10-0 = 859
Marca: x4 = (e4 + e5)/2 = (840 + 859)/2 = 857
Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 840 + 4·5 = 860
Subintervalo Superior: e6 = a + 5h - 10-d = 840 + 5·5 - 10-0 = 864
Marca: x5 = (e5 + e6)/2 = (840 + 864)/2 = 862
Sexto Intervalo.
Subintervalo Inferior: e6 = a + 5h = 840 + 5·5 = 865
Subintervalo Superior: e7 = a + 6h - 10-d = 840 + 6·5 - 10-0 = 869
Marca: x6 = (e6 + e7)/2 = (840 + 869)/2 = 867
La frecuencia absoluta será el número de veces que aparecen datos en los respectivos intervalos calculados anteriormente.
Para ello, empezamos a contar cuantos datos están dentro de cada intervalo de la tabla de datos original del problema, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi |
| 840 – 844 | 842 | 7 |
| 845 – 849 | 847 | 5 |
| 850 – 854 | 852 | 10 |
| 855 – 859 | 857 | 10 |
| 860 – 864 | 862 | 6 |
| 865 – 869 | 867 | 2 |
Una vez obtenidas las frecuencias absolutas, se obtienen las frecuencias absolutas acumuladas.
Las frecuencias absolutas acumuladas se obtienen aplicando la siguiente expresión:
· Fi = Σfi
Es decir, la frecuencia absoluta acumulada del primer subintervalo será igual a su frecuencia absoluta.
En cambio, la frecuencia absoluta acumulada del segundo subintervalo, será la suma de la frecuencia absoluta del intervalo anterior más la frecuencia absoluta suya.
Y así será la forma de proceder, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi |
| 840 – 844 | 842 | 7 | 7 |
| 845 – 849 | 847 | 5 | 12 |
| 850 – 854 | 852 | 10 | 22 |
| 855 – 859 | 857 | 10 | 32 |
| 860 – 864 | 862 | 6 | 38 |
| 865 – 869 | 867 | 2 | 40 |
Una vez obtenidas las frecuencias absolutas de los respectivos subintervalos, calculamos la frecuencia relativa:
· hi = fi/N
Para ello, se sabe que los datos originales, sin agrupar, hacen un total de N = 40.
Por lo tanto, las frecuencias relativas se muestran en la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi | Frecuencia Relativa, hi |
| 840 – 844 | 842 | 7 | 7 | 0.175 |
| 845 – 849 | 847 | 5 | 12 | 0.125 |
| 850 – 854 | 852 | 10 | 22 | 0.25 |
| 855 – 859 | 857 | 10 | 32 | 0.25 |
| 860 – 864 | 862 | 6 | 38 | 0.15 |
| 865 – 869 | 867 | 2 | 40 | 0.05 |
Ahora, se calcula las frecuencias relativas acumuladas. Para ello, aplicaremos la siguiente expresión:
· Hi = Fi/N
Teniéndose en cuenta que N = 40 (Número total de datos originales del problema)
Por lo tanto, aplicando la anterior expresión, completamos la tabla tal como sigue:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi | Frecuencia Relativa, hi | Frecuencias Absolutas Relativas, Hi |
| 840 – 844 | 842 | 7 | 7 | 0.175 | 0.175 |
| 845 – 849 | 847 | 5 | 12 | 0.125 | 0.3 |
| 850 – 854 | 852 | 10 | 22 | 0.25 | 0.55 |
| 855 – 859 | 857 | 10 | 32 | 0.25 | 0.8 |
| 860 – 864 | 862 | 6 | 38 | 0.15 | 0.95 |
| 865 – 869 | 867 | 2 | 40 | 0.05 | 1 |
Una vez obtenidos los datos agrupados y sus respectivas frecuencias, nos piden calcular la media, la mediana y la cuasi desviación típica.
Recordemos que el número total de datos es N = 40.
Datos Agrupados.
La media para datos agrupados se calcula mediante la siguiente expresión:
Sustituimos valores para obtener su valor:
· Fk > N/2
· Fk-1 < N/2
La clase 3 es la que cumple con las condiciones: N/2 = 40/2 = 20. La clase que cumple dicha desigualdad, es la del subintervalo, Fk, 850 – 854 con una frecuencia absoluta de f = 10 y el subintervalo, Fk-1, 845 – 849, con una frecuencia absoluta acumulativa de Fk = 12.
Y la expresión de la mediana para datos agrupados es la siguiente, sustituimos valores:
Para la cuasi desviación típica, se usa la siguiente expresión:
Apartado b)
Los límites, para este apartado, quedan definidos de la
siguiente manera:
· b = 868
Tomamos las clases que nos indica el enunciado: p = 7.
Una vez dispuesto los límites del intervalo, calculamos la longitud:
No hace falta redondear el valor de h ya que es igual al número de cifras decimales que poseen los datos de la muestra, por lo tanto,
· d = 0
Y ya se está listo para realizar los intervalos y las marcas del mismo:
Primer Intervalo.
Subintervalo Inferior: e1 = a = 840
Subintervalo Superior: e2 = a + h - 10-d = 840 + 4 - 10-0 = 843
Marca: x1 = (e1 + e2)/2 = (840 + 843)/2 = 857.5
· Segundo Intervalo.
Subintervalo Inferior: e2 = a + h = 840 + 4 =844
Subintervalo Superior: e3 = a + 2h - 10-d = 840 + 2·4 - 10-0 = 847
Marca: x2 = (e2 + e3)/2 = (844 + 847)/2 = 845.5
· Tercer Intervalo.
Subintervalo Inferior: e3 = a + 2h = 840 + 2·4 = 848
Subintervalo Superior: e4 = a + 3h - 10-d = 840 + 3·4 - 10-0 = 851
Marca: x3 = (e3 + e4)/2 = (848 + 851)/2 = 849.5
Cuarto Intervalo.
Subintervalo Inferior: e4 = a + 3h = 840 + 3·4 = 852
Subintervalo Superior: e5 = a + 4h - 10-d = 840 + 4·4 - 10-0 = 855
Marca: x4 = (e4 + e5)/2 = (852 + 855)/2 = 853.5
Quinto Intervalo.
Subintervalo Inferior: e5 = a + 4h = 840 + 4·4 = 856
Subintervalo Superior: e6 = a + 5h - 10-d = 840 + 5·4 - 10-0 = 859
Marca: x5 = (e5 + e6)/2 = (856 + 859)/2 = 857.5
Sexto Intervalo.
Subintervalo Inferior: e6 = a + 5h = 840 + 5·4 = 860
Subintervalo Superior: e7 = a + 6h - 10-d = 840 + 6·4 - 10-0 = 863
Marca: x6 = (e6 + e7)/2 = (860 + 863)/2 = 861.5
Séptimo Intervalo.
Subintervalo Inferior: e7 = a + 6h = 840 + 6·4 = 864
Subintervalo Superior: e8 = a + 7h - 10-d = 840 + 7·4 - 10-0 = 867
Marca: x7 = (e7 + e8)/2 = (864 + 867)/2 = 865.5
Hay que tener en cuenta, que la última clase se ha ampliado ligeramente, por ello, es mayor que las clases anteriores como nos hacía preveer el enunciado.
Esto es así, para poder tener agrupado el último dato en una de las clases.
La frecuencia absoluta será el número de veces que aparecen datos en los respectivos intervalos calculados anteriormente.
Para ello, empezamos a contar cuantos datos están dentro de cada intervalo de la tabla de datos original del problema, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi |
| 840 – 843 | 841.5 | 7 |
| 844 – 847 | 845.5 | 5 |
| 848 – 851 | 849.5 | 3 |
| 852 – 855 | 853.5 | 9 |
| 856 – 859 | 857.5 | 8 |
| 860 – 863 | 861.5 | 6 |
| 864 – 868 | 866 | 2 |
Una vez obtenidas las frecuencias absolutas, se obtienen las frecuencias absolutas acumuladas.
Las frecuencias absolutas acumuladas se obtienen aplicando la siguiente expresión:
· Fi = Σfi
Es decir, la frecuencia absoluta acumulada del primer subintervalo será igual a su frecuencia absoluta.
En cambio, la frecuencia absoluta acumulada del segundo subintervalo, será la suma de la frecuencia absoluta del intervalo anterior más la frecuencia absoluta suya.
Y así será la forma de proceder, obteniéndose la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi |
| 840 – 843 | 841.5 | 7 | 7 |
| 844 – 847 | 845.5 | 5 | 12 |
| 848 – 851 | 849.5 | 3 | 15 |
| 852 – 855 | 853.5 | 9 | 24 |
| 856 – 859 | 857.5 | 8 | 32 |
| 860 – 863 | 861.5 | 6 | 38 |
| 864 – 868 | 866 | 2 | 40 |
Una vez obtenidas las frecuencias absolutas de los respectivos subintervalos, calculamos la frecuencia relativa:
· hi = fi/N
Para ello, se sabe que los datos originales, sin agrupar, hacen un total de N = 40.
Por lo tanto, las frecuencias relativas se muestran en la siguiente tabla:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi | Frecuencia Relativa, hi |
| 840 – 843 | 841.5 | 7 | 7 | 0.175 |
| 844 – 847 | 845.5 | 5 | 12 | 0.125 |
| 848 – 851 | 849.5 | 3 | 15 | 0.075 |
| 852 – 855 | 853.5 | 9 | 24 | 0.225 |
| 856 – 859 | 857.5 | 8 | 32 | 0.2 |
| 860 – 863 | 861.5 | 6 | 38 | 0.15 |
| 864 – 868 | 866 | 2 | 40 | 0.05 |
Ahora, se calcula las frecuencias relativas acumuladas. Para ello, aplicaremos la siguiente expresión:
· Hi = Fi/N
Teniéndose en cuenta que N = 40 (Número total de datos originales del problema)
Por lo tanto, aplicando la anterior expresión, completamos la tabla tal como sigue:
| Subintervalos | Marca | Frecuencia Absoluta, fi | Frecuencia Absoluta Acumulada, Fi | Frecuencia Relativa, hi | Frecuencia Absoluta Relativa, Hi |
| 840 – 843 | 841.5 | 7 | 7 | 0.175 | 0.173 |
| 844 – 847 | 845.5 | 5 | 12 | 0.125 | 0.3 |
| 848 – 851 | 849.5 | 3 | 15 | 0.075 | 0.375 |
| 852 – 855 | 853.5 | 9 | 24 | 0.225 | 0.6 |
| 856 – 859 | 857.5 | 8 | 32 | 0.2 | 0.8 |
| 860 – 863 | 861.5 | 6 | 38 | 0.15 | 0.95 |
| 864 – 868 | 866 | 2 | 40 | 0.05 | 0.1 |
Una vez obtenidos los datos agrupados y sus respectivas frecuencias, nos piden calcular la media, la mediana y la cuasi desviación típica.
Recordemos que el número total de datos es N = 40.
Datos Agrupados.
La media para datos agrupados se calcula mediante la siguiente expresión:
· Fk > N/2
· Fk-1 < N/2
La clase que cumple dicha desigualdad, es la del subintervalo, Fk, 852 – 855 con una frecuencia absoluta de f = 9 y el subintervalo, Fk-1, 848 – 851, con una frecuencia absoluta acumulativa de Fk = 15.
Y la expresión de la mediana para datos agrupados es la siguiente, sustituimos valores:
Para la cuasi desviación típica, se usa la siguiente expresión:

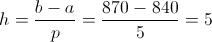
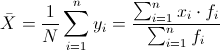





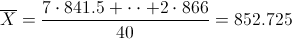






0 comentarios:
Publicar un comentario