Ej12. Un almacén, recibió 1000 botellas de vino. La probabilidad de que se rompa una botella durante el transporte es de 0.003.
Halla la probabilidad de que el almacén haya recibido rotas:
a) Dos botellas.
b) Menos de dos botellas.
c) Más de dos botellas.
d) Por lo menos una botella.
Este problema es un claro ejemplo de “éxito” o “fracaso”, por lo tanto, se empleará la expresión de la distribución binomial para hallar la solución del problema.
Donde:
p = 0.003: Probabilidad de éxito, una botella se rompa.
n = 1000: Número de botellas.
x: Depende de apartado, probabilidad de la variable aleatoria.
Se define la variable aleatoria:
X Ξ “Número de botellas rotas”.
Hay que tener en cuenta, que aunque sea una distribución binomial, ésta se puede aproximar a una distribución de Poisson, ya que:
n es muy grande.
n·p = 1000·0.003 = 3 ≤ 7.
Por lo tanto: λ = n·p = 3.
Apartado a)
Por lo tanto, la probabilidad de obtener dos botellas rotas con las condiciones indicadas, es de, aproximadamente, 0.224042.
Apartado b)
P(X < 2) = P(X = 0) + P(X = 1)
Por lo tanto, la probabilidad de obtener menos de dos botellas rotas con las condiciones indicadas, es de, aproximadamente, 0.199148.
Apartado c)
P(X > 2) = 1 - P(X ≤ 2) = 1 - P(X = 0) - P(X = 1) - P(X = 2)
Por lo tanto, la probabilidad de obtener más de dos botellas rotas con las condiciones indicadas, es de, aproximadamente, 0.576810.
Apartado d)
P(X ≥ 1) = 1 - P(X < 1) = 1 - P(X = 0)
Usando los valores de los apartados anteriores, se resuelve este apartado:
P(X ≥ 1) = 1 - P(X = 0) = 1 – 0.04979 = 0.95021
Por lo tanto, la probabilidad de obtener al menos una botella rota con las condiciones indicadas, es de, aproximadamente, 0.95021.

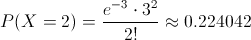
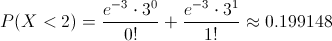
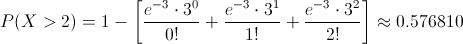




0 comentarios:
Publicar un comentario