Ej15. La probabilidad de que la calibración de un transductor en un instrumento electrónico cumpla con las especificaciones del sistema de medición es de 0.6. Si los intentos de calibración son independientes, ¿cuál es la probabilidad de que se requieran como máximo tres intentos para satisfaces las especificaciones del sistema de medición?.
Para hallar este problema, se usará la distribución geométrica:
Donde:
p: Probabilidad de que el instrumento cumple las especificaciones, es de 0.6.
x: Denota los intentos hasta lograr cumplir las especificaciones, en este caso 3.
Se usa la distribución geométrica porque es una serie de ensayos independientes buscando un éxito, en este caso, realizar ensayos de calibración hasta cumplir con las especificaciones.
Se define la variable aleatoria:
X Ξ “Número de ensayos hasta cumplir las especificaciones”.
Por lo tanto, tenemos que:
P(X) = P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)
Se usa la expresión de la distribución geométrica, con x = 1, para obtener la probabilidad de que al primer ensayo se satisfaga las especificaciones, obteniéndose:
P(X = 1) = 0.6·(1 - 0.6)1⁻¹ = 0.6
Se usa la expresión de la distribución geométrica, con x = 2, para obtener la probabilidad de que al segundo ensayo se satisfaga las especificaciones, obteniéndose:
Se usa la expresión de la distribución geométrica, con x = 3, para obtener la probabilidad de que al segundo ensayo se satisfaga las especificaciones, obteniéndose:
Por lo tanto:
P(X) = P(X ≤ 3) = 0.6 + 0.24 + 0.096 = 0.936
Otra forma alternativa de realizar este problema, es desarrollando el sumatorio:
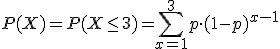
Obteniéndose:
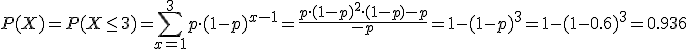
Quedando demostrado lo que se deseaba demostrar.





4 comentarios:
Eres un autentico maquina. Muchas felicitaciones por esta pedazo de pagina, imposible encontrar una mejor.
Saludos y que siga abierta mucho tiempo.
Desdeluego que eres el mejor...!! Muchas gracias por todo!!
buenas y de antemano las gracias por un blog tan util.
Mi duda es la siguiente al calcular la probabilidad P(X ≤ 3)
no deberia tenerse en cuenta tambien la probabilidad de P(X=0)
gracias y perdona las molestias
Buenas:
Te pongo la definición de la Distribución Geométrica que tenemos en este blog:
<< Es una serie de ensayos de Bernoulli independientes, con probabilidad constante p de un éxito, sea que la variable aleatoria X denote el número de ensayos hasta el primer éxito >>.
Donde pone: ... hasta el primer éxto, si te das cuenta, la Distribución Geométrica siempre va asociada a obtener un primer éxito/fracaso, es por ello que en el experimento X = 0 no puede haber ningún tipo de éxito/fracaso ya que no se ha iniciado el estudio todavía.
Otra manera de verlo es en su expresión matemática:
· P(X = x) = p·(1 - p)^(x - 1)
Si X = 0:
· P(X = 0) = p·(1 - p)^(- 1)
El exponente es negativo, esto indicaría que estamos analizando un estado del experimento anterior al propio inicio del experimento.
Por lo tanto, el la Distribución Geométrica, siempre se empieza desde X = 1.
Un saludo y gracias por tú
comentario.
Publicar un comentario