Ej19. En una cierta escuela, el 4% de los alumnos y el 1% de las alumnas, tienen una estatura superior a 1.90m. Además, el 60% de los estudiantes son mujeres. Se selecciona al azar un estudiante y su estatura resulta ser mayor de 1.90.
Halle la probabilidad de que sea mujer.
Ordenamos los datos, definimos los sucesos:
· A Ξ 'Ser alumna'
· B Ξ 'Medir más de 1.90m'
La probabilidad del suceso A según el problema es de 0.6, por lo tanto, se puede hallar la probabilidad de ser alumno:
La probabilidad de ser alumno es de 0.4.
El problema también, nos facilita las probabilidades de ser mayor de 1.90m, dado que sea alumna:
Y dado que sea alumno:
Ambas son probabilidades condicionales.
Una vez aclarados los datos que el problema nos ofrece, debemos resolver que al escoger un alumno al azar y ser éste mayor de 1.90m su estatura, que sea mujer.
Se resuelve usando el Teorema de Bayes. Para ello, es necesario saber todos los casos posibles que de escoger un estudiante al azar, éste sea mayor de 1.90m su estatura, no es más que obtener la probabilidad del suceso B, para ello, se usa la probabilidad total:
Por lo tanto, para saber qué probabilidad hay de que la seleccionada fuese alumna, es:

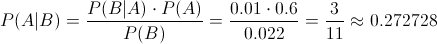




0 comentarios:
Publicar un comentario