Ej2. Para el experimento aleatorio de lanzamiento de dos dados, se define la variable aleatoria X como “el menor de los dos números obtenidos”.
Halla y represente gráficamente las funciones de probabilidad y distribución. Calcula la media y la varianza de X.
El espacio muestral del experimento de lanzar dos dados, es el siguiente:
Ω = {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}
Donde el primer elemento corresponde al primer dado, y el segundo al segundo dado, por ejemplo:
12:
1 → Primer dado.
2 → Segundo dado.
El espacio muestral contiene 36 elementos, la probabilidad de salir cualquier par de datos, es la misma, por lo tanto tienen una probabilidad de 1/36.
La variable aleatoria definida por el enunciado, X, “el menor de los números obtenidos”, hallamos su función de probabilidad:
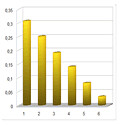
El menor sea un 1, X = 1: Existen 11 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 1. Por lo tanto, su probabilidad es:
P(X = 1) = 11/36
El menor sea un 2, X = 2: Existen 9 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 2. Por lo tanto, su probabilidad es:
P(X = 2) = 9/36
El menor sea un 3, X = 3: Existen 7 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 3. Por lo tanto, su probabilidad es:
P(X = 3) = 7/36
El menor sea un 4, X = 4: Existen 5 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 4. Por lo tanto, su probabilidad es:
P(X = 4) = 5/36
El menor sea un 5, X = 5: Existen 3 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 5. Por lo tanto, su probabilidad es:
P(X = 5) = 3/36
El menor sea un 6, X = 6: Existen 1 posibilidades entre todos los elementos del espacio muestral de que el menor valor sea un 6. Por lo tanto, su probabilidad es:
P(X = 6) = 1/36
Representamos gráficamente la función de probabilidad:
Donde el Eje X son los posibles valores de la variable aleatoria X, y el Eje Y, es la probabilidad que toma dicha variable aleatoria en los puntos correspondientes.
Una vez obtenida la función de probabilidades para cada caso, pasamos a obtener su función de distribución (o función de probabilidad acumulada):
El menor sea un 1, F(1) = P(X ≤ 1) = 11/36
El menor sea un 2, F(2) = F(1) + P(X = 2) = 11/36 + 9/36 = 20/36
El menor sea un 3, F(3) = F(2) + P(X = 3) = 20/36 + 7/36 = 27/36
El menor sea un 4, F(4) = F(3) + P(X = 4) = 27/36 + 5/36 = 32/36
El menor sea un 5, F(5) = F(4) + P(X = 5) = 32/36 + 3/36 = 35/36
El menor sea un 6, F(6) = F(5) + P(X = 6) = 35/36 + 1/36 = 1
Representamos gráficamente la función de distribución:
Una vez calculadas la función de probabilidad y representada gráficamente, y la función de distribución y representada también, pasamos a obtener la media y la varianza.
Para la media, usamos la expresión de la esperanza:
Por lo tanto, la esperanza es:
Para la varianza, usamos la siguiente expresión:
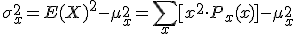
Obteniéndose:






0 comentarios:
Publicar un comentario