Problema3. VAD.

Ej3. Sea X una variable aleatoria que representa el número de clientes que llega a una tienda en un periodo de una hora, con probabilidades:

x	0	1	2	3	4	5	6	7	8
P(x)	0.05	0.1	0.1	0.1	0.2	0.25	0.1	0.05	0.05

Calcular:

a) E(X).

b) Var(X).

Apartado a)

Para hallar la media, es decir, la esperanza matemática, usamos la siguiente expresión:

E(X) = Σx·P_x(x)

Por lo tanto, la esperanza es:

E(X) = 0·0.05 + 1·0.1 + 2·0.1 + 3·0.1 + 4·0.2 + 5·0.25 + 6·0.1 + 7·0.05 + 8·0.05 = 4

Apartado b)

Para la varianza, usamos la siguiente expresión:

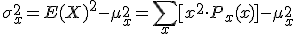
Obteniéndose:

σ²(X) = [0²·0.05 + 1²·0.1 + 2²·0.1 + 3²·0.1 + 4²·0.2 + 5²·0.25 + 6²·0.1 + 7²·0.05 + 8²·0.05] - 4² = 4.1