Problema4. VAD.

Ej4. Se dispone de una caja con cinco cartas numeradas así: 1, 1, 2, 2, 3 con la que realizamos el experimento aleatorio consistente en extraer al azar dos cartas. Asociadas a este experimento tenemos la variable aleatoria X = “suma de los números que figuran en las dos cartas”.

a) Obtén la función de probabilidad de X.

b) Calcula su valor esperado y su varianza.

El subconjunto de la variable aleatoria X es:

X = {1+1, 1+2, 1+2, 1+3, 1+1, 1+2, 1+2, 1+3, 2+1, 2+1, 2+2, 2+3, 2+1, 2+1, 2+2, 2+3, 3+1, 3+1, 3+2, 3+2}

Donde el primer término corresponde a la primera carta y el segundo término a la segunda carta.

Sumamos y reorganizamos el subconjunto de la variable X, obteniendo:

X = {2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5}

Existen 20 elementos que componen el subconjunto de la variable aleatoria X.

Apartado a)

Hallamos la función de probabilidad:

La suma de las dos cartas sea 2, X = 2: Existen 2 posibilidades entre todos los elementos. Por lo tanto, su probabilidad es:

P(X = 2) = 2/20

La suma de las dos cartas sea 3, X = 3: Existen 8 posibilidades entre todos los elementos. Por lo tanto, su probabilidad es:

P(X = 3) = 8/20

La suma de las dos cartas sea 4, X = 4: Existen 6 posibilidades entre todos los elementos. Por lo tanto, su probabilidad es:

P(X = 4) = 6/20

La suma de las dos cartas sea 5, X = 5: Existen 4 posibilidades entre todos los elementos. Por lo tanto, su probabilidad es:

P(X = 5) = 4/20

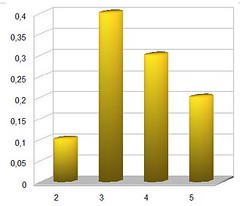
Una representación gráfica de la función de distribución es la siguiente:

Donde el Eje X es los posibles valores que toma la variable aleatoria X, y el Eje Y es la probabilidad en dichos puntos.

Apartado b)

Para hallar la media, es decir, la esperanza matemática, usamos la siguiente expresión:

E(X) = Σx·P_x(x)

Por lo tanto, la esperanza es:

E(X) = 2·2/20 + 3·8/20 + 4·6/20 + 5·4/20 = 3.6

Para la varianza, usamos la siguiente expresión:

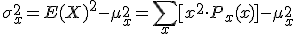
Obteniéndose:

σ²(X) = [2²·2/20 + 3²·8/20 + 4²·6/20 + 5²·4/20] - 3.6² = 0.84