Ej22. El número de camiones que pasan por delante de una gasolinera, con respecto al número de otros automóviles guarda una relación de 3 a 2. La probabilidad de que se detenga un camión a repostar es de 0.1, y para los otros automóviles es de 0.2.
¿Cuál es la probabilidad de que el próximo vehículo que venga a abastecerse sea un camión?
Se definen los sucesos:
A ≡ “Sea un camión”
B ≡ “Otros automóviles”
C ≡ “Repostar”
Según el enunciado, la probabilidad del suceso A es de 3/5, la probabilidad del suceso B es 2/5.
Y la probabilidad de que reposte dado que sea un camión es 0.1, análogamente, la probabilidad de que reposte dado que no sea un camión es de 0.2. En nomenclatura condicional:
· P(C|A) = 0.1
· P(C|B) = 0.2
El problema nos pide hallar la probabilidad de que el próximo vehículo que reposte sea un camión.
Esto es un claro ejemplo del Teorema de Bayes. Para ello, necesitamos saber la probabilidad de todos los vehículos que repostan, es decir, la probabilidad del suceso C, para ello, se aplica la probabilidad total:
Por lo tanto, la probabilidad de que el próximo vehículo a repostar sea un camión es:

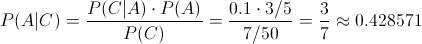




0 comentarios:
Publicar un comentario