Ej23. Se dispone de tres partidas de piezas, cada una con 20 ejemplares. El número de piezas normalizadas es, en la primera, segunda y tercera partidas, igual respectivamente a 20, 15 y 10. De una partida al azar, se ha tomado, también al azar, una pieza que ha resultado ser normalizada. Después de restituir la pieza a la partida, se ha tomado al azar, de la misma, una segunda pieza que ha resultado también normalizada.
Halle la probabilidad de que las dos piezas extraídas lo hayan sido de la tercera partida.
· A ≡ “Partida 1”
· B ≡ “Partida 2”
· C ≡ “Partida 3”
Existen tres partidas de piezas, la probabilidad de escoger cualquier partida de piezas es 1/3.
El problema indica que se selecciona una pieza al azar y ésta está normalizada, después la restituye a las partidas y vuelve a coger otra pieza, la cual también está normalizada.
Se define el suceso:
· E ≡ “Par de partidas normalizadas”
En cada partida de piezas, hay 20 ejemplares, de los cuales están normalizados:
Partida de piezas 1 hay 20 normalizados.
Partida de piezas 2 hay 15 normalizados.
Partida de piezas 3 hay 10 normalizados.
Por lo tanto, la probabilidad de los sucesos definidos anteriormente son: P(E|A) = 1*1 = 1, P(E|B) = 15/20 * 15/20 = 9/16 y P(E|C) = 10/20 * 10/20 = 1/4.
La probabilidad del suceso E, es la probabilidad total de que las piezas sean normalizadas de todas las partidas.
Por lo tanto, la probabilidad del suceso E, mediante la expresión de la probabilidad total, es:
Sustituyendo valores:
Esto significa que la probabilidad total de piezas normalizadas de las partidas es de 29/48.
Si se quiere saber, la probabilidad de las partidas extraídas hallan sido de la partida 3, se usa el Teorema de Bayes. Adaptando la expresión general al problema:

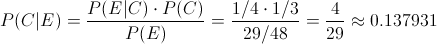




0 comentarios:
Publicar un comentario