Ej26. En un hospital especializado ingresa un promedio del 50% enfermos con la enfermedad K, del 30% con la enfermedad L y del 20% con la enfermedad M. La probabilidad de curación completa para estas enfermedades es, respectivamente, de 0.7, 0.8 y 0.9.
Calcule:
a) La probabilidad de curación para un enfermo que ingresa en el hospital.
b) Sabiendo que determinado enfermo se ha curado, halle la probabilidad de que padeciera la enfermedad K.
Se definen los sucesos:
· A ≡ 'Enfermos que padecen la enfermedad K'
· B ≡ 'Enfermos que padecen la enfermedad L'
· C ≡ 'Enfermos que padecen la enfermedad M'
· D ≡ 'Enfermos que se curan completamente'
Las probabilidades de los sucesos anteriores, según el enunciado del problema, son:
P(A) = 0.5, P(B) = 0.3 y P(C) = 0.2
El enunciado, nos ofrece también, datos de la probabilidad condicionada. La probabilidad de que un enfermo se cure dada la enfermedad K es P(D|A) = 0.7, la probabilidad de que un enfermo se cure dada la enfermedad L es P(D|B) = 0.8 y por último, la probabilidad de que un enfermo se cure dada la enfermedad M es de P(D|C) = 0.9.
Apartado a)
Para obtener la probabilidad del suceso D, se utiliza la expresión de la probabilidad total:
Apartado b)
Este apartado debemos resolver la probabilidad, sabiendo que determinado enfermo se ha curado de la enfermedad, que ésta fuera la K.
Como ya se ha obtenido la probabilidad de cura total en el anterior apartado, aplicamos el Teorema de Bayes:

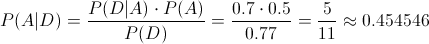




3 comentarios:
muy bueno
en el ejercicio que a mi me dan, tengo que hallar la probabilidad total de curados, y me dan que la enfermedad k es 0.3, la enfermedad L es 0.3, y la enfermedad M es 0.4, a demas me dan la proporcion de afectados con k y se curaron que es 0.7, y la proporcion de curados que estuvieron afectados por k= 0.6
es bastante parecido pero no se como hacerlo, alguien me puede ayudar por favor
Publicar un comentario