Ej27. Una planta ensambladora monta placas que contienen cada una un determinado microcircuito, el 50% de los cuales se lo compra al fabricante A, el 25% al fabricante B, y el restante 25%, al C. Se sabe que el porcentaje de circuitos defectuosos en los suministros de estos fabricantes es del 5%, el 10% y el 12% respectivamente.
a) Calcule la probabilidad de que una placa elegida al azar de entre las ensambladas en la planta, contenga un microcircuito defectuoso.
b) Si el microcircuito de una placa elegida al azar no está defectuoso, ¿cuál es la probabilidad de que se le haya comprado al fabricante B?
Se definen los sucesos:
· A ≡ 'Microcircuito fábrica A'
· B ≡ 'Microcircuito fábrica B'
· C ≡ 'Microcircuito fábrica C'
· D ≡ 'Circuitos defectuosos'
Las probabilidades de los sucesos anteriores, según el enunciado del problema, son:
P(A) = 0.5, P(B) = 0.25 y P(C) = 0.25
El enunciado, nos ofrece también, datos de la probabilidad condicionada. La probabilidad de que el microcircuito esté defectuoso dada la fábrica A es P(D|A) = 0.05, la probabilidad de que el microcircuito esté defectuoso dada la fábrica B es P(D|B) = 0.1 y por último, la probabilidad de que el microcircuito esté defectuoso dada la fábrica C es de P(D|C) = 0.12.
Apartado a)
Para obtener la probabilidad del suceso D, se utiliza la expresión de la probabilidad total:
Apartado b)
En este caso, el microcircuito no está defectuoso, se haya comprado al fabricante B es un claro ejemplo de Teorema de Bayes:
Se sustituye en la expresión del Teorema de Bayes:

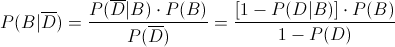
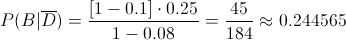




0 comentarios:
Publicar un comentario