Problema16: VAC

Ej16. Según una instantánea de E.U. (USA Snapshot), 26 de Octubre de 1994, el salario anual medio de un trabajador en Estados Unidos es de 26362$. Si se supone que los salarios anuales de los estadounidenses están distribuidos normalmente con una desviación estándar igual a 6500$, encuentre lo siguiente:

a) ¿Qué porcentaje gana menos de 15000$?.

b) ¿Qué porcentaje gana más de 40000$?


Sea la variable aleatoria X, salarios, en dólares, de trabajadores estadounidenses. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.

Cuya media es: 26362 y la desviación estándar: 6500.


Apartado a)

Nos piden obtener la siguiente probabilidad: P(X < . 15000)

Tipificamos los datos dados:

Operando la desigualdad:

P(Z <-1.748) = P(Z > 1.748) = 1 - P(Z ≤ 1.748) = 1 - [0.5 + Φ(1.748)]

En este caso, no se dispone del valor exacto en las tablas, por lo tanto, interpolamos linealmente:

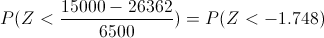
..1.74.............1.748..........1.75
0.4591............P.............0.4599

De donde:

0.4591 - 0.4599.-> 1.74 - 1.75
0.4591 - P..-> 1.74 - 1.748

Calculamos:

Por lo tanto, la solución a este apartado es:

P(Z < -1.748) = 0.5 - Φ(1.748) = 0.5 - 0.45974 = 0.04026

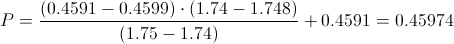
Apartado b)

Nos piden obtener la siguiente probabilidad: P(X >. 40000)

Tipificamos los datos dados:

Operando la desigualdad:

P(Z > 2.098) = 1 - P(Z ≤ 2.098) = 1 - [0.5 + Φ(2.098)]

Buscamos en las tablas de la Normal dicho valor, pero no tenemos el valor exacto, por lo que realizamos una interpolación lineal:

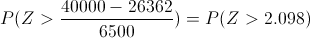
..2.09.............2.098..........2.10
0.4817............P.............0.4821

De donde:

0.4817 - 0.4821.-> 2.09 - 2.10
0.4817 - P..-> 2.09 - 2.098

Calculamos:

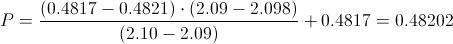
Por lo tanto, la solución a este apartado es:

P(Z > 2.098) = 0.5 - Φ(2.098) = 0.5 - 0.48202 = 0.01798