Ej17. En Estados Unidos, los pesos al nacer se distribuyen normalmente, con una media de 3420g y una desviación estándar de 495g. Si un hospital planea establecer condiciones especiales de observación para el 2% de los bebés menos pesados, ¿qué peso se utilizaría para establecer un punto de corte que separe al 2% de los bebés menos pesados de los demás?.
Sea la variable aleatoria X, pesos de los bebés estadounidenses. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 3420 y la desviación estándar: 495.
En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria X que lo satisfaga.
Tenemos: P(X < . x) = 0.02
Tipificamos:
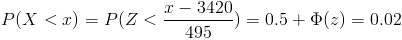
Despejamos:
Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay problema ya que son simétricos, por lo que buscamos en la tabla el valor 0.48 que de un z válido.
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..2.05.............Z..........2.06
0.4798........0.48.....0.4803
De donde:
0.4798 - 0.4803.-> 2.05 - 2.06
0.4798 - 0.48..-> 2.05 - Z
Calculamos:
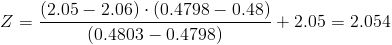
Por lo tanto, el peso de los bebés más pesados será de:
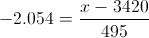
Despejamos x y obtenemos la solución a este problema: x = 2403.72





0 comentarios:
Publicar un comentario