Ej18. En un estudio de conducta facial, se toma el tiempo de contacto visual entre los participantes en un grupo de control, durante un período de 5 minutos. Los tiempos se distribuyen normalmente, con una media de 184.0 y una desviación estándar de 55.0 s (según datos de "Ethological Study of Facial Behavior in Nonparanoid and Paranoid Schizophrenic Patients", de Pittman, Olk, Orr y Singh, Psychiatry, vol. 144, núm. 1).
Para una persona elegida al azar del grupo de control, calcule la probabilidad de que el tiempo de contacto visual sea mayor que 230.0 s, que es la media de los esquizofrénicos paranoides.
Sea la variable aleatoria X, tiempo de contacto visual. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 184.0 y la desviación estándar: 55.0.
Nos piden obtener la siguiente probabilidad: P(X >. 230.0)
Tipificamos los datos dados:
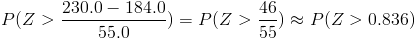
..0.83...........0.836..........0.84
0.2967............P............0.2995
De donde:
0.83 - 0.84.-> 0.2967 - 0.2995
0.83 - 0.836..-> 0.2967 - P
Calculamos:
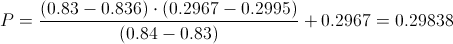





2 comentarios:
Los valores de tabla están errados
Revisa la tabla, en la acumulada cambian los valores y en los que aparecen son los de la tabla normal estandarizada.
Publicar un comentario