Problema19: VAC

Ej19. La duración de los embarazos se distribuye normalmente, con una media de 268 días y una desviación estándar de 15 días.

Obtener:

a) Un uso clásico de la distribución normal está inspirado por una carta dirigida a "Dear Abby", en la que una mujer afirmaba haber dado a luz 308 días después de una breve visita de su esposo, quien trabajaba en la Marina. Dada esta información, calcule la probabilidad de que un embarazo dure 308 días o más. ¿Qué sugiere tal resultado?.

b) Si estipulamos que un bebé es prematuro cuando la duración del embarazo se encuentra en el 4% inferior, calcule la duración que separa a los bebés prematuros de quellos que no lo son. Los bebés prematuros suelen requerir cuidados especiales y este resultado podría ser útil para los administradores de hospitales que planeen esos cuidados.

El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.

Cuya media es: 268 y la desviación estándar: 15.


Apartado a)

Sea la variable aleatoria X, duración del embarazo.

Nos piden obtener la siguiente probabilidad: P(X > 308)

Tipificamos los datos dados:

Operando la desigualdad:

P(Z > 2.67) = 1 - P(Z ≤ 2.67) = 1 - [0.5 + Φ(2.67)]

Buscamos en las tablas de la Normal dichos valores y resolvemos este apartado:

P(Z > 2.67) = 1 - [0.5 + 0.4962] = 0.0038

Este resultado sugiere que la duración del embarazo sea 308 días o mayor es muy poco ocurrente, puede ser que el esposo no sea el padre.

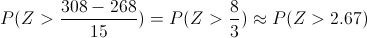
Apartado b)

Sea la variable aleatoria Y, bebés prematuros.

En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria Y que lo satisfaga.

Tenemos: P(Y < . y) = 0.04

Tipificamos:

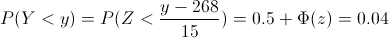
Despejamos:

Φ(z) = 0.04 - 0.5 = -0.46

Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay problema ya que son simétricos, por lo que buscamos en la tabla el valor 0.46 que de un z válido.

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.75.............Z..........1.76
0.4599........0.46.....0.4608

De donde:

0.4599 - 0.4608.-> 1.75 - 1.76
0.4599 - 0.46..-> 1.75 - Z

Calculamos:

Teniendo en cuenta que z se encuentra en la parte izquierda de la campana de Gauss, entonces: z = -1.751.

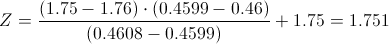
Por lo tanto, los bebés prematuros serán de:

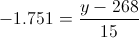
Despejamos y para obtener la solución a este problema: y = 241.735, es decir, para que un bebé sea prematuro debe nacer, aproximadamente, en 242 días o menos.