Ej20. Los ingenieros deben tomar en cuenta la anchura de las cabezas de los hombres cuando diseñan cascos para motocicletas. La anchura de las cabezas de los hombres se distribuyen normalmente, con una media de 6.0 in y una desviación estándar de 1.0 in (según datos de una encuesta antopométrica de Gordon, Churchill, et al.).
Debido a las limitaciones económicas, los cascos serán diseñados para que se ajusten a todos los hombres, excepto al 2.5% con anchuras más pequeñas, y al 2.5% con anchuras más grandes.
Calcule las anchuras de cabeza mínima y máxima que se ajustarán a los cascos.
El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 6.0 y la desviación estándar: 1.0.
Sea la variable aleatoria X, anchura de las cabezas de los hombres que se ajustarán a los cascos.
En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria X que lo satisfaga.
Tenemos: P(X < . x) = 0.025
Tipificamos:
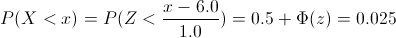
Despejamos:
Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay problema ya que son simétricos, por lo que buscamos en la tabla el valor 0.475 que de un z válido.
En la tabla, encontramos el valor exacto: z = 1.96, ahora bien, tenemos que tener en cuenta que la z válida está en el semieje negativo X: z = -1.96.
Por lo tanto, las anchuras de cabeza mínima serán:
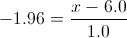
Despejamos x para obtener la solución a este problema: x = 4.04 pulgadas.
Tenemos: P(X >. x) = 0.025
Tipificamos:
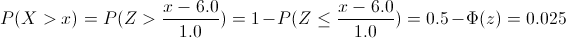
Despejamos:
Buscamos en la tabla el valor 0.475 que de un z válido.
En la tabla, encontramos el valor exacto: z = 1.96.
Por lo tanto, las anchuras de cabeza máxima serán:
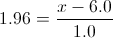
Despejamos x para obtener la solución a este problema: x = 7.96 pulgadas.
En resumen:
- Anchura de cabeza mínima: 4.04 in.
- Anchura de cabeza máxima: 7.96 in.





0 comentarios:
Publicar un comentario