Ej21. Una falla mecánica desapercibida ha provocado que 1/3 de la producción de una máquina de un taller de 5000 percutores de rifle estén defectuosos.
¿Cuál es la probabilidad de que un inspector encuentre no más de tres percutores de rifle defectuosos en una muestra de 25?.
Sea la variable aleatoria X, defectos en los percutores de rifle. Este es un claro ejemplo de acierto o error, por lo que estamos ante una distribución binomial: X ~ B(25, 1/3).
Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5: 25·1/3 ≈ 8.33 ≥ 5 OK.
2. n·q ≥ 5: 25·(1 - 1/3) ≈ 16.67 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
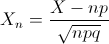
Por lo tanto: X ~
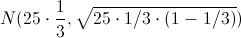 .
.Debemos calcular: P(X ≤ 3), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(X < . 3.5).
Tipificamos:
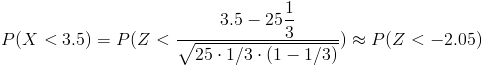
Operamos la desigualdad:
Buscamos en la tablas y sustituimos su valor para obtener la solución a este problema:





3 comentarios:
y si no se puede aproximar por la normal como se hace
Buenas:
Se resolvería como cualquier problema que contenga una variable aleatoria discreta que siga una distribución binomial:
· P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
Un saludo y gracias por tu comentario.
Me sirvió gracias
Publicar un comentario