Problema22: VAC

Ej22. Un fabricante de medicamentos afirma que sólo el 5% de los pacientes que usan una medicina en particular, experimentan efectos secundarios. Los médicos del hospital de una gran universidad usan este medicamento en el tratamiento de 250 pacientes.

¿Cuál es la probabilidad de que 15 o menos de los 250 pacientes experimenten efectos secundarios?.

Sea la variable aleatoria X, efectos secundarios al tomar una medicina en particular. Este es un claro ejemplo de acierto o error, por lo que estamos ante una distribución binomial: X ~ B(250, 0.05).

Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5: 250 · 0.05 ≈ 8.33 ≥ 5 OK.

2. n·q ≥ 5: 250·(1 - 0.05) ≈ 16.67 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

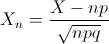
Por lo tanto: X ~ .

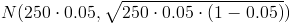Debemos calcular: P(X ≤ 15), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(X < . 15.5).

Tipificamos:

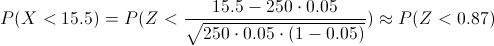
Por lo tanto:

P(Z < 0.87) = 0.5 + Φ(0.87)

Buscamos en la tablas y sustituimos su valor para obtener la solución a este problema:

P(Z < 0.87) = 0.5 + Φ(0.87) = 0.5 + 0.3078 = 0.8078