Ej23. No todos los entrenadores de la NBA de carrera larga, fueron constantes en cuanto a las temporadas ganadoras y los equipos que dirigieron. Por ejemplo, Bill Fitch, quién dirigió equipos de baloncesto profesional durante 25 temporadas después de iniciar su carrera como entrenador en la Universidad de Minnesota, ganó 944 encuentros, pero perdió 1106 mientras trabajó con los Cavaliers, los Celtics, los Rockets, los Nets y los Clipper (Sport Illustrated, "Who is Tim Floyd?", 3 de Agosto de 1998).
Si se elige aleatoriamente 60 resultados de los récords históricos de juegos en los que Bill Ficht dirigió a uno de los equipos participantes, ¿cuál es la probabilidad de que en menos de la mitad de esos encuentros su equipo sea el ganador?.
Sea la variable aleatoria X, victorias de un equipo de baloncesto. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:
· Partidos Ganados: 944
· Partidos Perdidos: 1106
Por lo tanto, el número total de partidos es: 944 + 1106 = 2050. Con este dato, podemos obtener las probabilidades de ganar o perder un partido:
· Probabilidad de Partidos Ganados: 944/2050 = 472/1025
· Probabilidad de Partidos Perdidos: 1106/2050 = 553/1025
Este es un claro ejemplo de acierto o error, en este caso, el acierto es partido ganado, por lo que estamos ante una distribución binomial: X ~ B(60, 472/1025).
Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5: 60 · 472/1025 ≈ 27.63 ≥ 5 OK.
2. n·q ≥ 5: 60 · 553/1025 ≈ 32.37 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
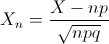
Por lo tanto: X ~
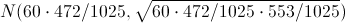 .
.Debemos calcular: P(X < . 30), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(X < . 29.5).
Tipificamos:
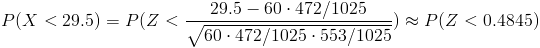
Por lo tanto, la solución a este problema es:
En este caso, no se dispone del valor exacto en las tablas, por lo tanto, interpolamos linealmente:
..0.48...........0.4845.......0.49
0.1844............P............0.1879
De donde:
0.48 - 0.49.-> 0.1844 - 0.1879
0.48 - 0.4845.-> 0.1844 - P
Calculamos:
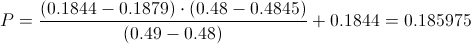
Sustituyendo valores, obtenemos la solución a este apartado:





5 comentarios:
bill fitch hizo campeon a boston celtics en 1982, donde estaba el gran larry bird. dos veces entrenador del año. quinto entrenador con mas victorias en la nba pero el segundo con mas derrotas. :)
¡Buen dato!
Gracias por tu comentario.
Y no seria esto una variable aleatoria discreta?
Es decir...si es una variable aleatoria discreta con una distribucion binomial, se aproximaria a Poisson no a la normal
Buenas:
Como puedes ver en la solución del problema, la variable aleatoria que se presenta es una variable aleatoria discreta que sigue una distribución Binomial.
Pero, al ser los datos dados bastante grandes, se comprueba si se puede aproximar a una variable continua, en este caso, a una distribución Normal.
Es cierto que trabajando dentro del ámbito de las variables aleatorias discretas, una binomial se puede aproximar a una Poisson si se cumplen ciertas condiciones.
Lo que pasa, que es más fácil trabajar con variables continuas (en teoría), y el error que se comete es mínimo (siempre y cuando se cumplan las condiciones idóneas para la aproximación).
Un saludo.
Publicar un comentario