Problema2: Cartas de Control

Ej2. Los datos de la siguiente tabla se obtuvieron de un proceso de fabricación de fuentes de tensión. La característica de calidad es la tensión (en voltios) de la fuente, y las muestras empleadas para la inspección eran de tamaño 5.

Muestra	X	R		Muestra	X	R
1	103	4		11	105	4
2	102	5		12	103	2
3	104	2		13	102	3
4	105	11		14	105	4
5	104	4		15	104	5
6	106	3		16	105	3
7	102	7		17	106	5
8	105	2		18	102	2
9	106	4		19	105	4
10	104	3		20	103	2

Determinar:

a) Los límites de control y la línea central de la carta X.

b) Suponiendo que la característica de calidad tiene una distribución normal, estima la desviación típica del proceso.

c) Traza la gráfica de control X, ¿está el proceso bajo control?


Apartado a)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Se desconoce μ y σ.
· Tamaño de la muestra: n = 5.
· Número de muestras: m = 20.

Nos piden obtener la carta de control de medias X, cuyos límites de control son:

·

·

·

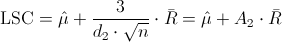
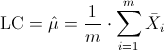
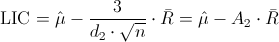
Donde A₂ y d₂, están tabulados para varios valores de n, en nuestro caso, n = 5, consultamos en la tabla:

· A₂ = 0.577
· d₂ = 2.326

Siendo:

·

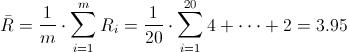
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de medias X, empezamos por la línea central:

·

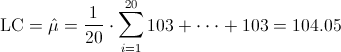
Y posteriormente, obtenemos los límites superior e inferior de control:

· LSC = μ + A₂·R = 104.05 + 0.577·3.95 = 106.32915
· LIC = μ - A₂·R = 104.05 - 0.577·3.95 = 101.77085

Como resumen, los límites de control para la carta X son:

· LSC = 106.32915
· LC = 104.05
· LIC = 101.77085


Apartado b)

Por definición:

Sigma: σ = R/d₂ = 3.95/2.326 ≈ 1.698194


Apartado c)

Debemos representar la carta de control de medias X, pero antes, debemos obtener los límites σ y 2σ de las mismas, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, vamos a calcular el valor de σ para obtener los límites de control de advertencia.

Por el apartado anterior: σ = R/d₂ = 3.95/2.326 ≈ 1.698194

Por lo tanto, los límites de advertencia de control 2σ son:

· X + 2·σ/√n = 104.05 + 2·1.698194/√5 ≈ 105.568911
· X - 2·σ/√n = 104.05 - 2·1.698194/√5 ≈ 102.531089

Para los límites de advertencia de control σ son:

· X + σ/√n = 104.05 + 1.698194/√5 ≈ 104.809455
· X - σ/√n = 104.05 - 1.698194/√5 ≈ 103.290545

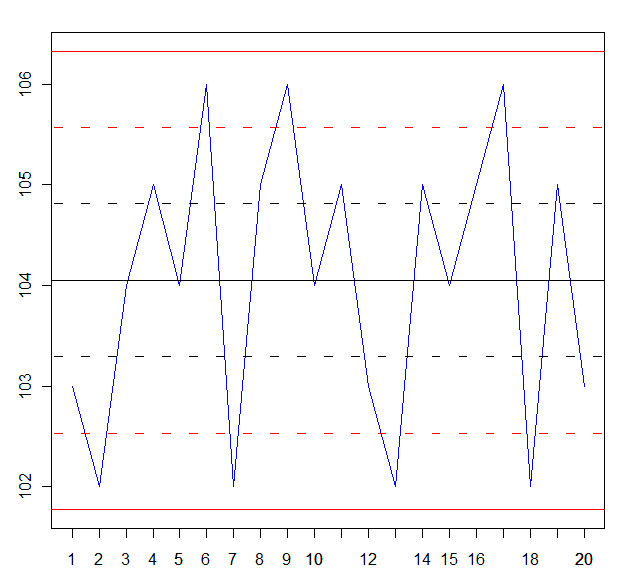
Y en este momento, estamos en disposición de realizar la gráfica de control X:

Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que todos los puntos están dentro de los límites de control 3σ.

Pero el proceso está fuera de control ya que existen 2 de 3 puntos consecutivos que se encuentra a una distancia más allá de los límites 2σ. Los puntos son:

· 5: LC
· 6: 2σ
· 7: 2σ

Por lo tanto, el proceso X está fuera de control.