Ej3. Una compañía de productos electrónicos fabrica tubos de rayos catódicos. Con objeto de controlar el proceso, durante 21 días de cierto mes, se muestrearon cada día 50 tubos de la línea de producción y se inspeccionaron. En la siguiente tabla, se presenta el número de tubos defectuosos encontrados cada día:
| Día | Tubos Defectuosos | Día | Tubos Defectuosos | |
| 1 | 11 | 12 | 23 | |
| 2 | 15 | 13 | 15 | |
| 3 | 12 | 14 | 12 | |
| 4 | 10 | 15 | 11 | |
| 5 | 9 | 16 | 11 | |
| 6 | 12 | 17 | 16 | |
| 7 | 12 | 18 | 15 | |
| 8 | 14 | 19 | 10 | |
| 9 | 9 | 20 | 13 | |
| 10 | 13 | 21 | 12 | |
| 11 | 15 |
Determinar:
a) Los límites de control y la línea central de la carta p de la fracción de tubos de rayos catódicos defectuosos.
b) Traza la gráfica de control p, ¿está el proceso bajo control?.
c) En caso de que el proceso esté fuera de control, recalcula los límites de control omitiendo los datos que caen fuera de los límites 3-σ.
Apartado a)
Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:
· Carta de control p, fracción de defectos.
· Tamaño de la muestra: n = 50.
· Número de muestras: m = 21.
Nos piden obtener la carta de control de fracción de defectos p, cuyos límites de control son:
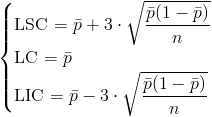
Siendo:
·
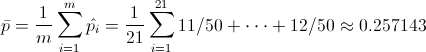
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de fracción defectuosos, p:
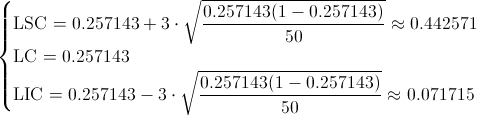
Apartado b)
Debemos representar la carta de control p, de fracción de tubos de rayos catódicos defectuosos, pero antes, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.
Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.
En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.
- Para el límite superior:
(LSC - LC)/3 = (0.442571 - 0.257143)/3 ≈ 0.061809
Por lo tanto, los límites de advertencia de control 2σ son:
· p + 2·σ = 0.257143 + 2·0.061809 = 0.380761
Para los límites de advertencia de control σ son:
· p + σ = 0.257143 + 0.061809 = 0.318952
- Para el límite inferior:
(LC - LIC)/3 = (0.257143 - 0.071715)/3 ≈ 0.061809
Por lo tanto, los límites de advertencia de control 2σ son:
· p - 2·σ = 0.257143 - 2·0.061809 = 0.133525
Para los límites de advertencia de control σ son:
· p - σ = 0.257143 - 0.061809 = 0.195334
Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.
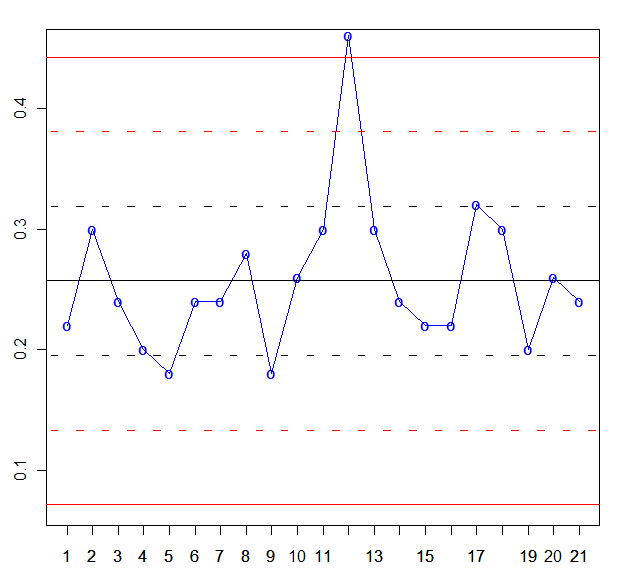
Y en este momento, estamos en disposición de realizar la gráfica de control p:
Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que un punto, el número 12, está fuera de los límites de control 3σ, por lo tanto, el proceso está fuera de control.
Apartado c)
El proceso contiene un punto, concretamente el punto 12, fuera de los límites de control, el enunciado nos dice que lo eliminemos y recalculemos los límites de control nuevamente.
· Carta de control p, fracción de defectos.
· Tamaño de la muestra: n = 50.
· Número de muestras: m = 20.
Nos piden obtener la carta de control de fracción de defectos p, cuyos límites de control son:
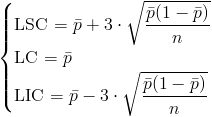
Siendo:
·
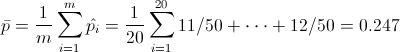
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de fracción defectuosos, p:
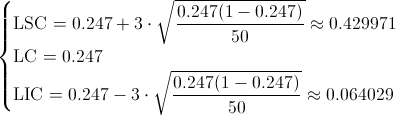
Debemos representar la carta de control p, de fracción de tubos de rayos catódicos defectuosos, pero antes, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.
Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.
En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.
- Para el límite superior:
Por lo tanto, los límites de advertencia de control 2σ son:
· p + 2·σ = 0.247 + 2·0.060990 = 0.36898
Para los límites de advertencia de control σ son:
· p + σ = 0.247 + 0.060990 = 0.30799
- Para el límite inferior:
Por lo tanto, los límites de advertencia de control 2σ son:
· p - 2·σ = 0.247 - 2·0.060990 = 0.12502
Para los límites de advertencia de control σ son:
· p - σ = 0.247 - 0.060990 = 0.18601
Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.
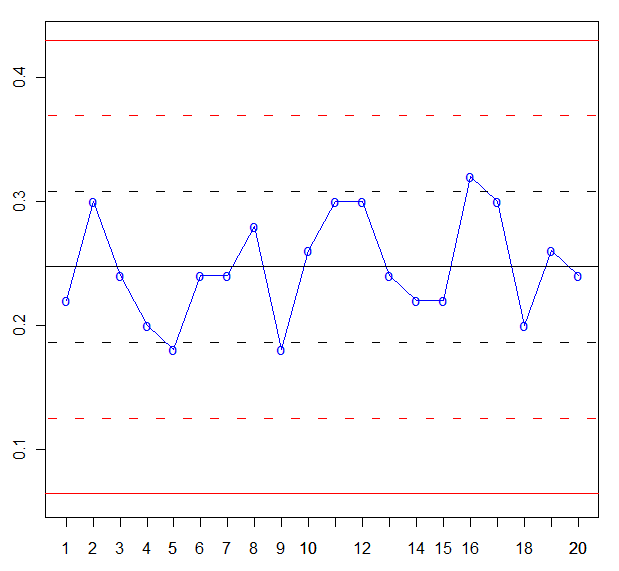
Y en este momento, estamos en disposición de realizar la gráfica de control p:
Podemos observar que el proceso está bajo control ya que cumple con todas las premisas necesarias.
A veces, la técnica de eliminar un punto concreto que hace que el proceso completo esté fuera de control es útil, ya que se haya podido dar por causas ajenas al propio proceso y es un momento único y aislado.
Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.
En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.
- Para el límite superior:
(LSC - LC)/3 = (0.429971 - 0.247)/3 ≈ 0.060990
Por lo tanto, los límites de advertencia de control 2σ son:
· p + 2·σ = 0.247 + 2·0.060990 = 0.36898
Para los límites de advertencia de control σ son:
· p + σ = 0.247 + 0.060990 = 0.30799
- Para el límite inferior:
(LC - LIC)/3 = (0.247 - 0.064029)/3 ≈ 0.060990
Por lo tanto, los límites de advertencia de control 2σ son:
· p - 2·σ = 0.247 - 2·0.060990 = 0.12502
Para los límites de advertencia de control σ son:
· p - σ = 0.247 - 0.060990 = 0.18601
Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.
Y en este momento, estamos en disposición de realizar la gráfica de control p:
Podemos observar que el proceso está bajo control ya que cumple con todas las premisas necesarias.
A veces, la técnica de eliminar un punto concreto que hace que el proceso completo esté fuera de control es útil, ya que se haya podido dar por causas ajenas al propio proceso y es un momento único y aislado.





0 comentarios:
Publicar un comentario